VariogramFunction

VariogramFunction

SpatialEstimateのオプションで，使用する局所変動モデルを指定する．

詳細

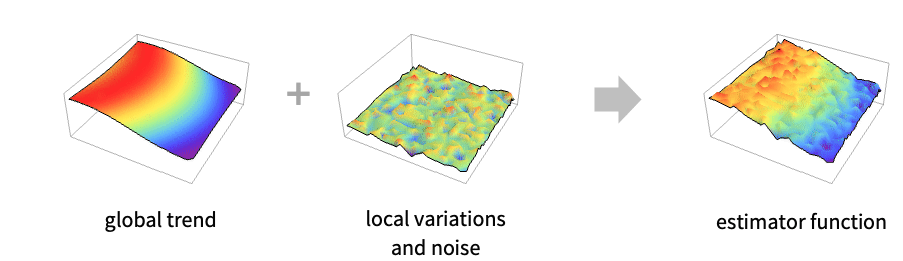
  • VariogramFunctionをSpatialNoiseLevelと一緒に使って空間値の局所予測を行うことができる．局所予測をグローバルトレンドと組み合せると完全な空間予測関数が与えられる．
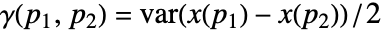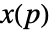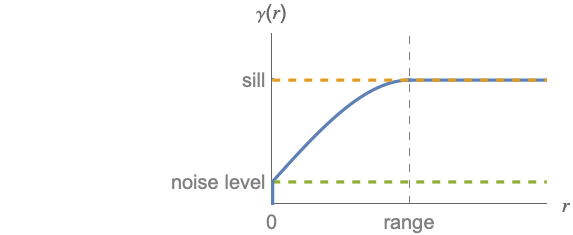
  • 局所変動はバリオグラム を使って説明される．ただし，は値の空間場である．空間場が弱定常で等方性のときは gamma(p_1,p_2)=gamma(TemplateBox[{{{p, _, 1}, -, {p, _, 2}}}, Norm])である．典型的な等方性バリオグラムは，そのシル，範囲，ノイズ分散で説明できる．
  • 完全な詳細については，EstimatedVariogramModelページを参照のこと．
  • 次は，使用可能な設定である．
  • Automaticバリオグラムを自動計算する
    "model""model"バリオグラムをフィットする
    {"model",pars}"model"を与えられたパラメータ pars で使う
    VariogramModel[…]完全に指定されたバリオグラムモデルを使う
  • 使用可能な"model"の値はVariogramModelで与えられる．

例題

すべて開くすべて閉じる

例  (1)

SpatialEstimateを指定されたバリオグラム関数と一緒に使う：

スイスの降雨観測のデータ：

指数関数バリオグラムモデルで空間予測関数を作成する：

観測領域上で推測値を可視化する：

スコープ  (1)

SpatialEstimateをフィットされたバリオグラム関数と一緒に使う：

このデータはスイスにおける降雨観察からなっている：

三次元バリオグラムモデルをフィットして空間予測に使う：

フィットされた三次元バリオグラムモデルで予測関数を計算する：

アプリケーション  (1)

SpatialEstimateでVariogramFunctionを指定することでモデルの表が得られる：

データを可視化する：

特定のモデルを使って推定値を計算する：

ランダムな点の集合を作成し，それらの場所における推定値を計算する：

領域全体の降雨量を可視化する：

Wolfram Research (2021), VariogramFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/VariogramFunction.html.

テキスト

Wolfram Research (2021), VariogramFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/VariogramFunction.html.

CMS

Wolfram Language. 2021. "VariogramFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VariogramFunction.html.

APA

Wolfram Language. (2021). VariogramFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VariogramFunction.html

BibTeX

@misc{reference.wolfram_2025_variogramfunction, author="Wolfram Research", title="{VariogramFunction}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/VariogramFunction.html}", note=[Accessed: 26-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_variogramfunction, organization={Wolfram Research}, title={VariogramFunction}, year={2021}, url={https://reference.wolfram.com/language/ref/VariogramFunction.html}, note=[Accessed: 26-April-2025 ]}