初期値および境界値問題

はじめに非線形初期値問題と境界値問題
線形初期値問題と境界値問題区分係数初期値問題

はじめに

DSolveでは，主に微分方程式や微分方程式系の一般解を見付けることができる．一般解は，問題の完全な解空間の構造についての情報を与える．しかし，実際には，応用分野に関連した条件を満足する特殊解のみが知りたいという場合もよくある．このような条件には通常次のような2つの種類がある．

  • ある単独の点における特殊値を知るために，，のような解 および／またはその導関数が必要とされる．この場合，系は固定された初期値（この場合は0）から進化し始めると仮定されるため，このような問題は初期値問題(IVP)と呼ばれる．
  • 1対の点における特殊値を知るために，および のような 解が必要とされる．この場合，点0および1は，その応用において関心のある領域の境界点（線）とみなされるため，このような問題は境界値問題(BVP)と呼ばれる．

初期値問題と境界値問題のどちらの記号解法でも，問題の一般解が分かっていなければならない．初期値，境界値を使って特殊解を得るという最終段階は，ほとんど代数的に操作され，初期値問題に対するものと境界値問題に対するものは類似している．

線形微分方程式の初期値問題および境界値問題では，代数的操作の最終段階が線形方程式の解法であるため，かなり簡単に解くことができる．しかし，内在する方程式が非線形である場合，解にいくつかの分岐があったり，一般解の任意定数が超越関数の異なる引数に現れたりすることがある．その結果，非線形の問題では，最終の代数操作が常に完了できるとは限らない．また，内在する方程式に区分（不連続）係数がある場合，初期値問題は係数が連続となっている領域上で，自然に簡単な初期値問題へと分割される．

線形初期値問題と境界値問題

まず，一階線形常微分方程式の初期値問題を考える．

一階線形常微分方程式である：
一般解は，任意定数C[1]の線形関数である：
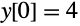
以下で，初期条件 に対する特殊解を求める：
解が方程式と初期条件の両方を満足することを検証する：
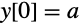
一般的な初期条件 での同じ問題を解いたときの解である：
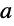
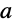
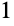
以下で， の異なる値に対する方程式の積分曲線をプロットする．このプロットにより，パラメータ がとの間にあるときは解は変曲点を持ち， が他の値のときは，最大値または最小値が生じることが分かる：
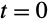
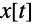
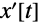
次は における と の初期値を指定した，二階線形方程式の解である：
解が方程式と初期条件を満足することを検証する：
解のプロットである：
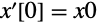
問題の解についての追加情報を得るためには，と設定する：
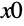
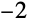
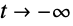
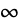
以下は，異なる初期方向に対する解のプロットである．の値が（常微分方程式の補助方程式の最大根）より小さいか大きいかによって，となるにつれて解はそれぞれあるいはに近付く：
二階非同次線形方程式の境界値問題である：

初期値問題とは対照的に，境界値が指定されているときは，一般存在定理も一意性定理もない．また，解がない場合もある．

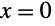
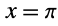
以下の問題では，一般解のC[2]の項が と の両方で消滅するため，解はない．従ってパラメータC[1]に対して矛盾した条件が2つあり，解は空集合になる：

既述の線形方程式の説明は，高階線形常微分方程式と線形常微分方程式系に一般化される．

四階線形常微分方程式の初期値問題の解である：
解と初期条件を検証する：
これは四階常微分方程式なので，初期値問題の特殊解を見付けるためには，4つの独立条件を指定しなければならない．条件の数が不足している場合，DSolveが返す解には，以下のように任意パラメータがいくつか含まれることがある：
最後に，線形常微分方程式系の初期値問題の解である：
以下で解が系と初期条件を満足するかどうかを検証する：
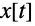
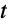
解 ，，は変数 でパラメータ化される．これらは，平面上で，あるいは空間の曲線として別々にプロットすることができる：

非線形初期値問題と境界値問題

多くの実世界の応用分野では，非線形常微分方程式の初期値および境界値問題の解が必要とされる．その例として，人口動態で使われるロジスティック方程式を考えてみる．

ロジスティック方程式である：
方程式の右辺はy[t]の二次方程式に展開することができる．このように，ロジスティック方程式は単なるリッカティ方程式であり，その一般解は簡単に見付けることができる：
以下で内的自然増加率rを1/2に，飽和水準Kを4に設定して，初期値問題を解く．
これは，記号パラメータrおよびKを持つロジスティック方程式の初期値問題を解く：
解が方程式と初期条件を満足するかどうかを検証する：
rとKの値を変更したときの解のプロットである：
以下は二階非線形常微分方程式の初期値問題の例である．この方程式の一般解は，陽形式で得ることができる：
解が方程式と初期条件を満足するかどうかを検証する：
最後に，二階非線形常微分方程式の境界値問題である．解は0および無限において境界条件を満足しなければならない．メッセージSolve::ifunは，一般解をEllipticFの逆関数であるJacobiSNで見付けるときに生成される．メッセージDSolve::bvlimが生じるのは，条件y′[Infinity]0を満足するために必要とされる極限が，一般解のどちらの分岐に対しても計算できないためである．しかし，境界値問題の解は，一般解の定数C[1]とC[2]の値を決定する別の方法を使って見付けられる：

非線形方程式の初期値あるいは境界値問題の記号解は，常に求められるとは限らない．そのような場合は，数値解法が必要となることがある．

区分係数初期値問題

現代の応用分野で生じる微分方程式は，不連続係数を持つことがよくある．DSolveは広範に渡るそのような区分係数常微分方程式を扱うことができる．このような方程式で使われる関数の中にはUnitStep，Max，Min，Sign，Abs等がある．これらの関数およびその組合せはPiecewiseオブジェクトに変換することができる．

指定された式がPiecewise式に変換される：
UnitStepを含む一階常微分方程式の一般解である：
上と同じ常微分方程式で，初期条件がある場合の解である：
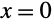
解は通常通りにプロットできる．解は連続であるが，では微分できない：
解を検証する：
次は係数にMaxを含む区分常微分方程式である：

区分常微分方程式は，係数および境界条件の式が区間ごとに変化するような，分離した区間上の常微分方程式の集合と考えることができる．従って，区間ごとに異なる解があり，常微分方程式の最終解は，異なる区間上の解を継ぎ合せて求める．

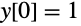
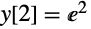
以下の区間常微分方程式では，FinalSolの式がSolFromMinusInfinityToTwoとSolFromTwoToInfinityとを継ぎ合せることで得られている．区間(-Infinity,2] の境界条件は単に であるが，区間[2,Infinity)の初期条件は （最初の区間の解の最終値で与えられる）である：

問題に多数の不連続があれば，問題の公式で直接Piecewiseを使うと便利である．

下の二階常微分方程式にはPiecewise項が含まれている：
この常微分方程式にはClip関数が含まれている．解は，エアリー関数で与えられる：