Introduction to Differential Equation Solving with DSolve
The Wolfram Language function DSolve finds symbolic solutions to differential equations. (The Wolfram Language function NDSolve, on the other hand, is a general numerical differential equation solver.) DSolve can handle the following types of equations:
- Ordinary Differential Equations (ODEs), in which there is a single independent variable
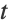 and one or more dependent variables
and one or more dependent variables 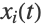 . DSolve is equipped with a wide variety of techniques for solving single ODEs as well as systems of ODEs.
. DSolve is equipped with a wide variety of techniques for solving single ODEs as well as systems of ODEs. - Partial Differential Equations (PDEs), in which there are two or more independent variables and one dependent variable. Finding exact symbolic solutions of PDEs is a difficult problem, but DSolve can solve most first-order PDEs and a limited number of the second-order PDEs found in standard reference books.
- Differential-Algebraic Equations (DAEs), in which some members of the system are differential equations and the others are purely algebraic, having no derivatives in them. As with PDEs, it is difficult to find exact solutions to DAEs, but DSolve can solve many examples of such systems that occur in applications.
| DSolve[eqn,y[x],x] | solve a differential equation for y[x] |
| DSolve[{eqn1,eqn2,…},{y1[x],y2[x],…},x] | |
| solve a system of differential equations for yi[x] | |
Finding symbolic solutions to ordinary differential equations.
DSolve returns results as lists of rules. This makes it possible to return multiple solutions to an equation. For a system of equations, possibly multiple solution sets are grouped together. You can use the rules to substitute the solutions into other calculations.
A general solution contains arbitrary parameters C[i] that can be varied to produce particular solutions for the equation. When an adequate number of initial conditions is specified, DSolve returns particular solutions to the given equations.
| DSolve[eqn,y,x] | solve a differential equation for y as a pure function |
| DSolve[{eqn1,eqn2,…},{y1,y2,…},x] | |
| solve a system of differential equations for the pure functions yi | |
Finding symbolic solutions to ordinary differential equations as pure functions.
When the second argument to DSolve is specified as y instead of y[x], the solution is returned as a pure function. This form is useful for verifying the solution of the ODE and for using the solution in further work. More details are given in "Setting Up the Problem".
| DSolve[eqn,u[x,y],{x,y}] | solve a partial differential equation for |
Finding symbolic solutions to partial differential equations.
While general solutions to ordinary differential equations involve arbitrary constants, general solutions to partial differential equations involve arbitrary functions. DSolve labels these arbitrary functions as C[i].
DSolve can also solve differential-algebraic equations. The syntax is the same as for a system of ordinary differential equations.
Goals of Differential Equation Solving with DSolve Tutorials
The design of DSolve is modular: the algorithms for different classes of problems work independently of one another. Once a problem has been classified (as described in "Classification of Differential Equations"), the available methods for that class are tried in a specific sequence until a solution is obtained. The code has a hierarchical structure whereby the solution of complex problems is reduced to the solution of relatively simpler problems, for which a greater variety of methods is available. For example, higher-order ODEs are typically solved by reducing their order to 1 or 2.
The process described is done internally and does not require any intervention from the user. For this reason, these tutorials have the following basic goals.
- To provide enough information and tips so that users can pose problems to DSolve in the most appropriate form and apply the solutions in their work. This is accomplished through a substantial number of examples. A summary of this information is given in "Working with DSolve".
- To give a catalog of the kinds of problems that can be handled by DSolve as well as the nature of the solutions for each case. This is provided in the tutorials on ODEs, PDEs, DAEs, and boundary value problems (BVPs).
These Differential Equation Solving with DSolve tutorials will be useful in acquiring a basic knowledge of DSolve and also serve as a ready reference for information on more advanced topics.