Symbolic Calculations with Units
Symbolic Calculations with Units
The Wolfram System's ability to deal with symbolic expressions, as well as numbers, allows you to use it for many kinds of mathematics. The Wolfram System's unit system utilizes this symbolic code base, facilitating calculus using Quantity expressions.
| Solve[equation,vars] | solution to an equation for x |
| Integrate[f,x] | the indefinite integral |
| D[f,x] | the (partial) derivative |
Some symbolic mathematical operations that operate on Quantity expressions.
Many symbolic commands are capable of understanding units. Still, there are times when you might wish to add or remove units. These can be handled by the Wolfram System's general substitution mechanism.
This assigns units to each symbol. Notice that the input symbols are dimensionful, but the output symbols are dimensionless:
A quick way to test whether an equation is dimensionally consistent is to subtract both sides, substitute in quantity values, and check whether it evaluates to a valid Quantity object:
These values are inconsistent with the equation, so messages are issued, and the computation returns only partially evaluated. As a result, the output has Head Plus:
This substitution replaces each quantity with just the numerical portion, leaving a purely symbolic expression:
Solve is aware of Quantity and will automatically determine the units of unknown variables within the equation. Units for variables can be specified by inserting the variable inside a Quantity expression with the desired units.
Units can be specified by entering the unknown variable as a Quantity:
If Solve cannot determine the units of an unknown variable, because of ambiguity or a dimensionality conflict, it will return unevaluated:
Integrate is aware of Quantity and will correctly combine the units of the integrand and integration variables. If the variable of integration is a Quantity object, then its QuantityMagnitude is used as the integration variable for performing the integration, and its QuantityUnit will be combined with the units of the integrand in the result. In general, it is best to enter the input in one of two forms:
1. The integrand and all the integration variables are Quantity objects.
2. Quantity objects only appear in the limits of definite integration.
Input can be entered in other ways, but Integrate will fail if it cannot determine a consistent assignment of units for all expressions. The assumed dimensions of the integration variable in definite integration will vary depending on how the variable and limits are expressed. For a specification like {x,Quantity[a,"unit1"],Quantity[b,"unit2"]}, x is assumed to have the same dimensions as "unit1" and "unit2". For a specification like {Quantity[x,"unit"],a,b}, x itself is generally assumed to be dimensionless. In this latter case, a and b must be quantities of the same dimensions as unit.
If the Quantity wrapper around t in the integrand is omitted, the final result will have dimensions 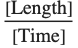 :
:
Integrate a linear charge density function. Notice that the whole integrand is a Quantity, allowing an easy combination of the units:
If the integration variables are not declared as quantities, and quantity objects in the integrand are constants, Integrate will maintain the separated form of the integrand:
When the integrand has nonconstant Quantity objects as subexpressions, Integrate must infer units from the various expressions. If these inferences lead to contradictions, Integrate will fail:
D is aware of Quantity and will correctly combine the units of Quantity objects in the expression being differentiated with the units of the differentiation variables.
D will automatically keep track of units:
Differentiate an expression containing several Quantity objects:
Computing a gradient with respect to Quantity variables:
Related Guides
-
▪
- Units