Simulation Center Tools—FFT Analysis
Simulation Center provides a number of tools for working with experiments and simulation results.
For a complete list, see the Tools guide.
Fast Fourier Transform (FFT) Analysis
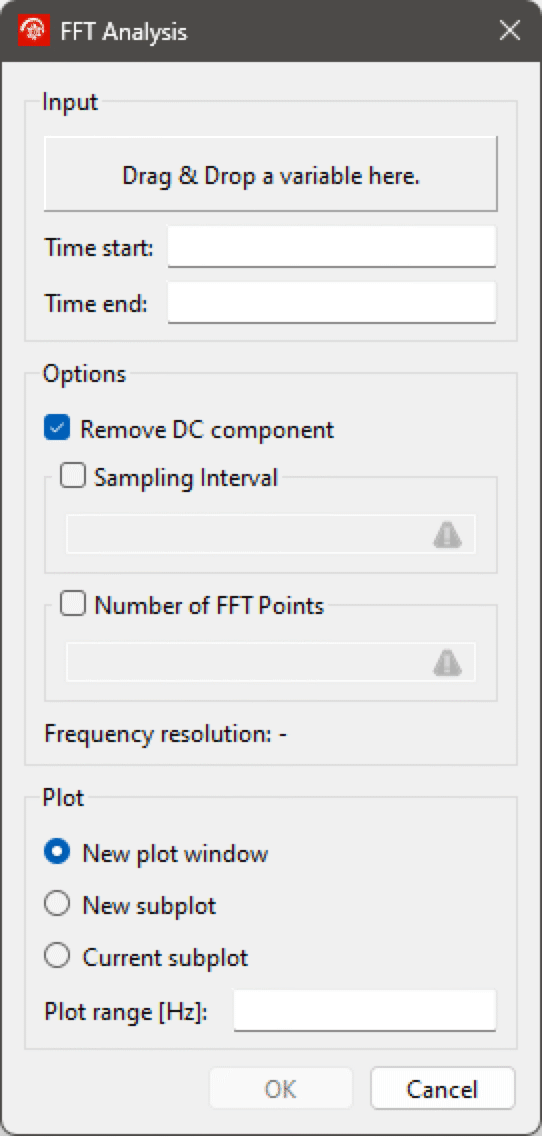
To perform an FFT analysis in Simulation Center, choose Tools ▶ FFT Analysis; this will bring up the FFT Analysis dialog. To select a variable for FFT analysis, switch to the Plot view of the Experiment Browser, then click and hold the right mouse button on the desired variable and drag it into the drop area in the FFT Analysis dialog. It is also possible to right-click on a variable in a plot window and choose FFT Analysis.
Options
If Remove DC component is checked, the mean value of the signal is removed before the FFT is done.
By default the FFT is performed over the time interval where the variable is defined. However, it is possible to define a custom time window by changing Time start and Time end.
Since the solver generally does not give equidistant output, the signal needs to be re-sampled. When Sampling Interval is unchecked, it will be determined by the length of the time window (i.e. Time end-Time start) divided by the number of intervals (i.e. Number of FFT Points-1) in that time window. The result is rounded down so that it remains in coherence with the next larger FFT size. This approach only works if the output intervals are almost equal; if the model has a large amount of events that are not uniformly distributed over the time window (e.g. they are clustered), it is recommended to select a custom sampling interval.
If a custom sampling interval is entered, the number of FFT points is calculated from the chosen sampling interval and vice versa. By using a custom sampling interval and a custom number of FFT points, it is possible to do a zero-padded FFT.
The FFT result can be plotted in a new plot window, a new subplot or in the current subplot. If a custom plot range is specified, the 
axis range will be adjusted accordingly. The FFT will be automatically recomputed whenever the experiment is resimulated. As with other plots, FFT plots can be stored as Model Plots.
