WOLFRAM SYSTEM MODELER
ConductorMultiphase linear conductor |
|
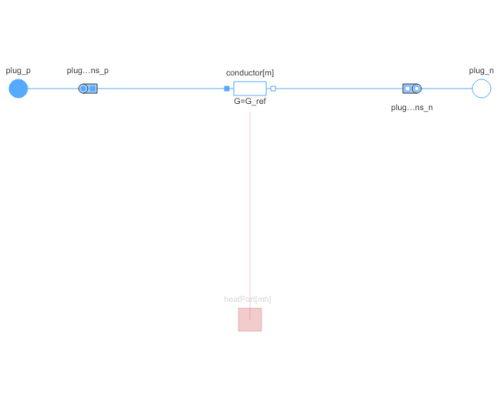
Diagram
Wolfram Language
SystemModel["Modelica.Electrical.QuasiStationary.MultiPhase.Basic.Conductor"]
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
The linear resistor connects the complex currents i with the complex
voltages v by v*G = i,
using m single phase Conductors.
The conductor model also has m optional
conditional heat ports.
A linear temperature dependency of the conductances for enabled heat ports is also taken into account.
See also
Conductor, Resistor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Parameters (6)
| mh |
Value: m Type: Integer Description: Number of heatPorts=number of phases |
|---|---|
| useHeatPort |
Value: false Type: Boolean Description: =true, if all heat ports are enabled |
| T |
Value: T_ref Type: Temperature[mh] (K) Description: Fixed device temperatures if useHeatPort = false |
| G_ref |
Value: Type: Conductance[m] (S) Description: Reference conductances at T_ref |
| T_ref |
Value: fill(293.15, m) Type: Temperature[m] (K) Description: Reference temperatures |
| alpha_ref |
Value: zeros(m) Type: LinearTemperatureCoefficient[m] (1/K) Description: Temperature coefficient of conductance (G_actual = G_ref/(1 + alpha_ref*(heatPort.T - T_ref)) |
Connectors (3)
| plug_p |
Type: PositivePlug Description: Positive quasi-static polyphase plug |
|
|---|---|---|
| plug_n |
Type: NegativePlug Description: Negative quasi-static polyphase plug |
|
| heatPort |
Type: HeatPort_a[mh] Description: Conditional heat ports |
Components (5)
| v |
Type: ComplexVoltage[m] Description: Complex voltage |
|
|---|---|---|
| i |
Type: ComplexCurrent[m] Description: Complex current |
|
| plugToPins_p |
Type: PlugToPins_p |
|
| plugToPins_n |
Type: PlugToPins_n |
|
| conductor |
Type: Conductor[m] |
Used in Examples (1)
|
Modelica.Magnetic.QuasiStatic.FundamentalWave.Examples.Components Comparison of equivalent circuits of eddy current loss models |