Information

This information is part of the Modelica Standard Library maintained by the Modelica Association.

Approximate calculation of the mean convective heat transfer coefficient kc for forced convection with a fully developed fluid flow in a turbulent regime.

Functions kc_approxForcedConvection and kc_approxForcedConvection_KC

There are basically three differences:

The function kc_approxForcedConvection is using kc_approxForcedConvection_KC but offers additional output variables like e.g. Reynolds number or Nusselt number and failure status (an output of 1 means that the function is not valid for the inputs).
Generally the function kc_approxForcedConvection_KC is numerically best used for the calculation of the mean convective heat transfer coefficient kc at known mass flow rate.
You can perform an inverse calculation from kc_approxForcedConvection_KC, where an unknown mass flow rate is calculated out of a given mean convective heat transfer coefficient kc

Restriction

Constant wall temperature or constant heat flux
Turbulent regime (Reynolds number 2500 < Re < 1e6)
Prandtl number 0.5 ≤ Pr ≤ 500

Calculation

The mean convective heat transfer coefficient kc is approximated through different Nusselt number Nu correlations out of [Bejan 2003, p. 424 ff].
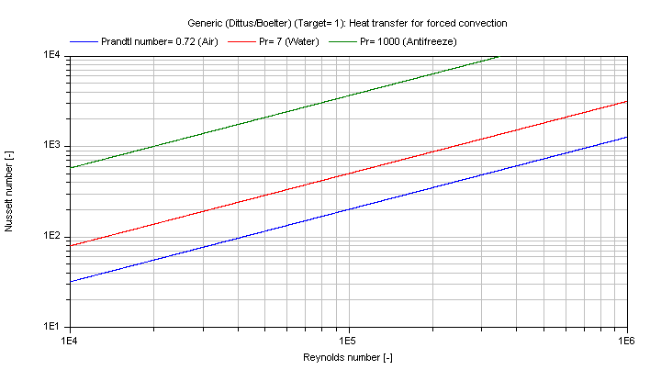
Roughest approximation according to Dittus/Boelter (1930):

Nu_1 = 0.023 * Re^(4/5) * Pr^(exp_Pr)

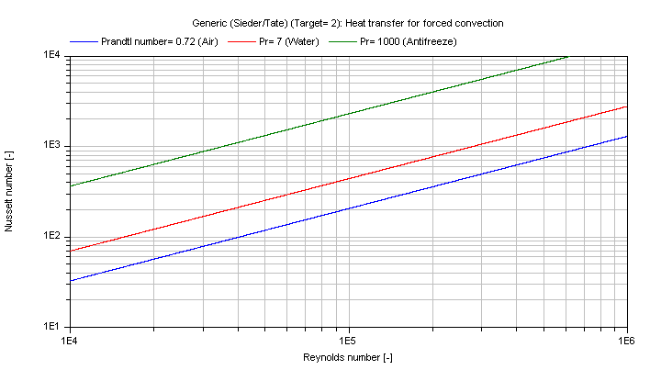
Middle approximation according to Sieder/Tate (1936) considering the temperature dependence of the fluid properties:

Nu_2 = 0.023 * Re^(4/5) * Pr^(1/3) * (eta/eta_wall)^(0.14)

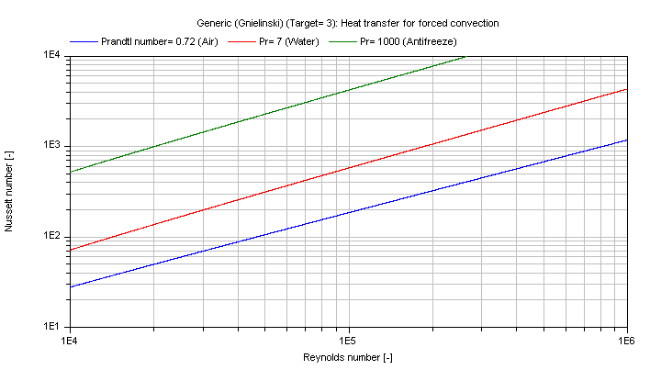
Finest approximation according to Gnielinski (1976):

Nu_3 = 0.0214 * [Re^(0.8) - 100] * Pr^(0.4) for Pr ≤ 1.5
     = 0.012 * [Re^(0.87) - 280] * Pr^(0.4) for Pr > 1.5

The mean convective heat transfer coefficient kc is calculated by:

kc =  Nu * lambda / d_hyd

with

eta	as dynamic viscosity of fluid [Pa.s],
eta_wall	as dynamic viscosity of fluid at wall temperature [Pa.s],
exp_Pr	as exponent for Prandtl number w.r.t. Dittus/Boelter (0.4 for heating or 0.3 for cooling) [-],
kc	as mean convective heat transfer coefficient [W/(m2.K)],
lambda	as heat conductivity of fluid [W/(m.K)],
d_hyd	as hydraulic diameter [m],
Nu_1/2/3	as mean Nusselt number [-],
Pr	as Prandtl number [-],
Re	as Reynolds number [-].

Verification

The mean Nusselt number Nu representing the mean convective heat transfer coefficient kc for Prandtl numbers of different fluids is shown in the figure below.

Dittus/Boelter (target = Modelica.Fluid.Dissipation.Utilities.Types.kc_general.Rough)

kc_approxForcedConvection_T1

Sieder/Tate (Target = Modelica.Fluid.Dissipation.Utilities.Types.kc_general.Middle)

kc_approxForcedConvection_T2

Gnielinski (Target = Modelica.Fluid.Dissipation.Utilities.Types.kc_general.Finest)

kc_approxForcedConvection_T3

Note that all fluid properties shall be calculated with the mean temperature of the fluid between the entrance and the outlet of the generic device.

References