Information

This information is part of the Modelica Standard Library maintained by the Modelica Association.

Calculation of the mean convective heat transfer coefficient kc of a helical pipe for turbulent flow regime.

Functions kc_turbulent and kc_turbulent_KC

There are basically three differences:

The function kc_turbulent is using kc_turbulent_KC but offers additional output variables like e.g. Reynolds number or Nusselt number and failure status (an output of 1 means that the function is not valid for the inputs).
Generally the function kc_turbulent_KC is numerically best used for the calculation of the mean convective heat transfer coefficient kc at known mass flow rate.
You can perform an inverse calculation from kc_turbulent_KC, where an unknown mass flow rate is calculated out of a given mean convective heat transfer coefficient kc

The critical Reynolds number Re_crit in a helical pipe depends on its mean curvature diameter. The smaller the mean curvature diameter of the helical pipe d_mean, the earlier the turbulent regime will start due to vortexes out of higher centrifugal forces.

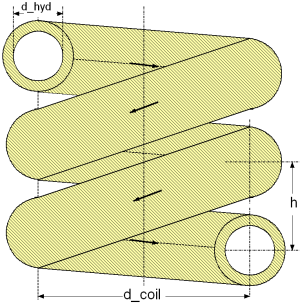
Geometry

helicalPipe

Calculation

The mean convective heat transfer coefficient kc for helical pipes is calculated through the corresponding Nusselt number Nu according to [VDI 2002, p. Ga 2, eq. 6]:

Nu = (zeta_TOT/8)*Re*Pr/{1 + 12.7*(zeta_TOT/8)^0.5*[Pr^(2/3)-1]},

where the influence of the pressure loss on the heat transfer calculation is considered through

zeta_TOT = 0.3164*Re^(-0.25) + 0.03*(d_hyd/d_coil)^(0.5) and

and the resulting mean convective heat transfer coefficient kc

kc =  Nu * lambda / d_hyd

with

d_mean	as mean diameter of helical pipe [m],
d_coil = f(geometry)	as mean curvature diameter of helical pipe [m],
d_hyd	as hydraulic diameter of the helical pipe [m],
h	as slope of helical pipe [m],
kc	as mean convective heat transfer coefficient [W/(m2K)],
lambda	as heat conductivity of fluid [W/(mK)],
L	as total length of helical pipe [m],
*Nu = kcd_hyd/lambda**	as mean Nusselt number [-],
*Pr = etacp/lambda**	as Prandtl number [-],
*Re = rhovd_hyd/eta*	as Reynolds number [-],
Re_crit = f(geometry)	as critical Reynolds number [-].

Verification

The mean Nusselt number Nu representing the mean convective heat transfer coefficient kc is shown below for different numbers of turns n_nt at constant total length of the helical pipe.

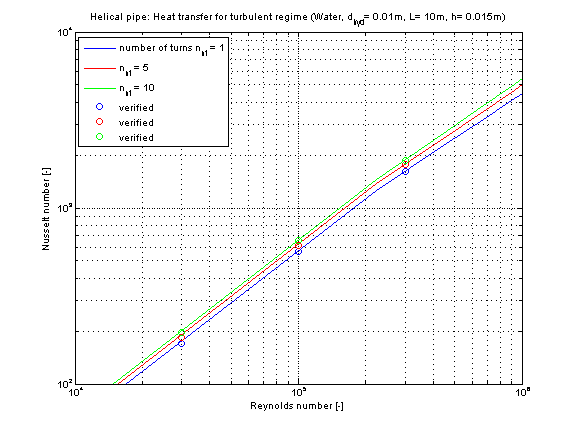
kc_turbulent

The convective heat transfer of a helical pipe is enhanced compared to a straight pipe due to occurring turbulences resulting out of centrifugal forces. The higher the number of turns, the better is the convective heat transfer for the same length of a pipe.

Note that the ratio of hydraulic diameter to total length of helical pipe d_hyd/L has no remarkable influence on the coefficient of heat transfer kc.

References