WOLFRAM SYSTEM MODELER
dp_edgedOverall |
|
Wolfram Language

SystemModel["Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.PressureLoss.Bend.dp_edgedOverall"]

Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Calculation of pressure loss in edged bends with sharp corners at overall flow regime for incompressible and single-phase fluid flow through circular cross sectional area considering surface roughness.
Restriction
This function shall be used inside of the restricted limits according to the referenced literature.
- circular cross sectional area [Idelchik 2006, p. 366, diag. 6-7]
- edged bend with sharp corners at turning [Idelchik 2006, p. 366, diag. 6-7]
- 0° ≤ angle of turning ≤ 180° [Idelchik 2006, p. 338, sec. 19]
- length of edged bend along edged axis / diameter ≥ 10 [Idelchik 2006, p. 366, diag. 6-7]
Geometry
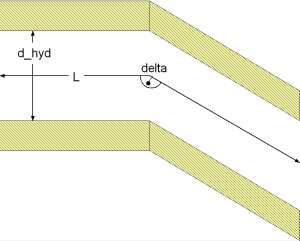
Calculation
The pressure loss dp for edged bends is determined by:
dp = zeta_TOT * (rho/2) * velocity^2
with
| rho | as density of fluid [kg/m3], |
| velocity | as mean velocity [m/s], |
| zeta_TOT | as pressure loss coefficient [-]. |
The pressure loss coefficient zeta_TOT of an edged bend can be calculated for different angles of turning delta by:
zeta_TOT = A * C1 * zeta_LOC * CF_Fri* CF_Re [Idelchik 2006, p. 366, diag. 6-7] and [Miller 1984, p. 149, sec. 9.4]
with
| A | as coefficient considering effect for angle of turning [-], |
| C1 | as coefficient considering relative elongation of cross sectional area (here: circular cross sectional area) [-], |
| CF_Fri | as correction factor considering surface roughness [-], |
| CF_Re | as correction factor considering Reynolds number [-], |
| delta | as angle of turning [deg]. |
The correction factor CF_Fri regarding the influence of surface roughness is determined as ratio of the Darcy friction factor for rough surfaces to smooth surfaces according to [Miller, p. 207, eq. 9.3]:
CF_Fri = lambda_FRI_rough / lambda_FRI_smooth
and the Darcy friction factors lambda_FRI are calculated with an approximated Colebrook-White law according to [Miller, p. 191, eq. 8.4]:
lambda_FRI = 0.25*(lg(K/(3.7*d_hyd) + 5.74/Re^0.9))^-2
with
| d_hyd | as hydraulic diameter [m], |
| K | as absolute roughness (average height of surface asperities) [m], |
| lambda_FRI | as Darcy friction factor[-], |
| Re | as Reynolds number [m], |
| zeta_TOT | as pressure loss coefficient [-]. |
Note that the Darcy friction factor for a smooth surface lambda_FRI_smooth is calculated with the previous equation and an absolute roughness of K = 0.
The correction for surface roughness through CF_Fri is used only in the turbulent regime, where the fluid flow is influenced by surface asperities not covered by a laminar boundary layer. Here the correction according to friction starts at Re ≥ Re_lam_leave according to [Idelchik 2006, p. 336, sec. 15]. Here the end of the laminar regime is restricted to a Reynolds number smaller than 2e3 w.r.t. [VDI, p. Lac 6, fig. 16].
Nevertheless the transition point from the laminar to the transition regime is shifted to smaller Reynolds numbers for an increasing absolute roughness. This effect is considered according to [Samoilenko in Idelchik 2006, p. 81, sec. 2-1-21] as:
Re_lam_leave = 754*exp(if k ≤ 0.007 then 0.0065/0.007 else 0.0065/k)
with
| k = K /d_hyd | as relative roughness [-], |
| Re_lam_leave | as Reynolds number for leaving laminar regime [-]. |
Note that the beginning of the laminar regime cannot be beneath Re ≤ 5e2.
In addition the influence or decreasing Reynolds numbers Re on the pressure loss coefficient zeta_TOT in the laminar and turbulent regime is considered through a second correction factor CF_Re according to [Miller 1984, p. 149, sec. 9.4] by:
CF_Re = B/Re^exp for Re ≤ 2e5
with
| B = f(Geometry) | as coefficient considering effect of Reynolds number in laminar regime [-], |
| exp | as exponent for Reynolds number in laminar regime [-], |
| Re | as Reynolds number [-], |
Note that the coefficient B considers the influence of the angle of turning delta on the pressure loss coefficient zeta_TOT in the laminar regime according to [Idelchik 2006, p. 340, sec. 28].
Note that the correction of the pressure loss coefficient zeta_TOT is influenced by the correction factor CF_Re only for decreasing Reynolds numbers Re out of the turbulent fluid flow regime at Re ≤ 2e5 into transition and laminar fluid flow regime.
Verification
The pressure loss coefficient zeta_TOT of a edged bend in dependence of the Reynolds number Re for different angles of turning delta is shown in the figures below.
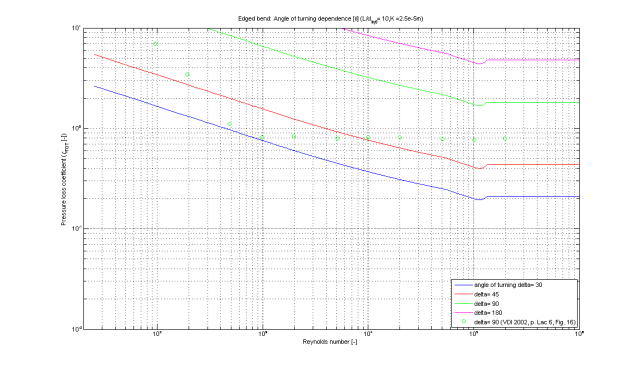
Pressure loss calculation of edged bends is complex and there are large differences in literature data. Nevertheless these calculations cover the usual range of pressure loss coefficients for an edged bend.
The validation of the pressure loss coefficient for an edged bends shows four possible flow regimes:
- laminar regime for Re ≤ 5e2
- transition regime for 5e2 ≤ Re ≤ 1e3 ... 1e4
- turbulent regime dependent on Reynolds number for 2e3 ... 1e4 ≤ Re ≤ 1e5
- turbulent regime independent of Reynolds number for Re ≥ 2e5
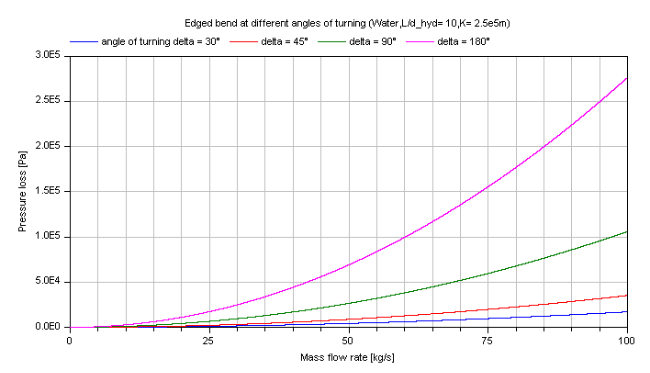
Incompressible case [Pressure loss = f(m_flow)]:
The pressure loss in dependence of the mass flow rate of water is shown for different angles of turning:
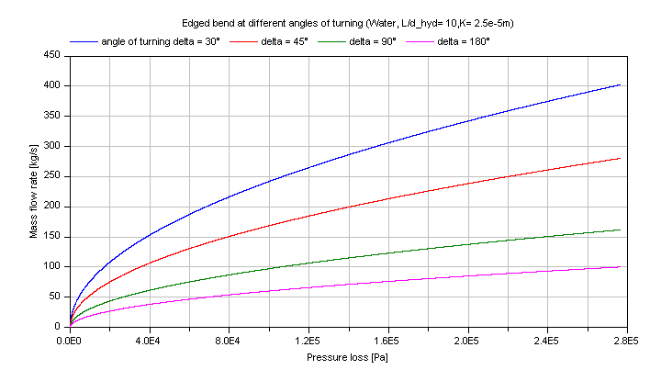
Compressible case [Mass flow rate = f(dp)]:
The mass flow rate in dependence of the pressure loss of water is shown for different angles of turning:
References
- Idelchik,I.E.:
- Handbook of hydraulic resistance. Jaico Publishing House,Mumbai,3rd edition, 2006.
- Miller,D.S.:
- Internal flow systems. volume 5th of BHRA Fluid Engineering Series.BHRA Fluid Engineering, 1984.
- Samoilenko,L.A.:
- Investigation of the hydraulic resistance of pipelines in the zone of transition from laminar into turbulent motion. PhD thesis, Leningrad State University, 1968.
- VDI:
- VDI - Wärmeatlas: Berechnungsblätter für den Wärmeübergang. Springer Verlag, 9th edition, 2002.
