Information

This information is part of the Modelica Standard Library maintained by the Modelica Association.

Restriction

This function shall be used within the restricted limits according to the referenced literature.

Smooth surface
Turbulent flow regime
Reynolds number for sudden expansion Re > 3.3e3 [Idelchik 2006, p. 208, diag. 4-1]
Reynolds number for sudden contraction Re > 1e4 [Idelchik 2006, p. 216-217, diag. 4-9]

Geometry

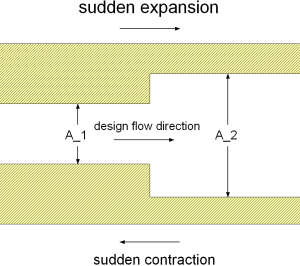
suddenChangeSection

Calculation

The local pressure loss dp is generally determined by:

dp = 0.5 * zeta_LOC * rho * |v_1|*v_1

with

rho	as density of fluid [kg/m3],
v_1	as average flow velocity in small cross sectional area [m/s].
zeta_LOC	as local resistance coefficient [-],

The local resistance coefficient zeta_LOC of a sudden expansion can be calculated for different ratios of cross sectional areas by:

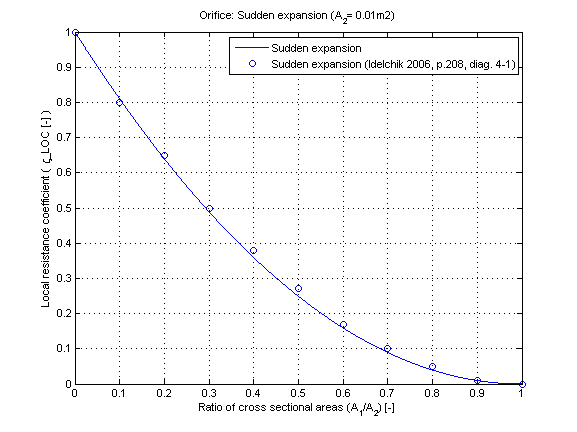
zeta_LOC = (1 - A_1/A_2)^2  [Idelchik 2006, p. 208, diag. 4-1]

and for sudden contraction:

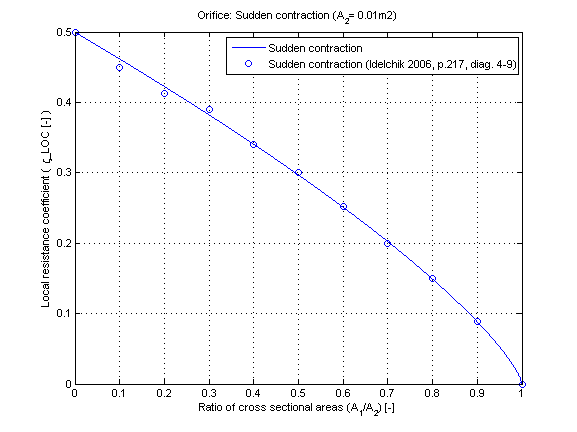
zeta_LOC = 0.5*(1 - A_1/A_2)^0.75  [Idelchik 2006, p. 216-217, diag. 4-9]

with

A_1	small cross sectional area [m^2],
A_2	large cross sectional area [m^2].

Verification

The local resistance coefficient zeta_LOC of a sudden expansion in dependence of the cross sectional area ratio A_1/A_2 is shown in the figure below.

suddenChangeExpansion

The local resistance coefficient zeta_LOC of a sudden contraction in dependence of the cross sectional area ratio A_1/A_2 is shown in the figure below.

suddenChangeContraction

References

Elmqvist, H., M.Otter and S.E. Cellier:: Inline integration: A new mixed symbolic / numeric approach for solving differential-algebraic equation systems.. In Proceedings of European Simulation MultiConference, Prague, 1995.
Idelchik,I.E.:: Handbook of hydraulic resistance. Jaico Publishing House, Mumbai, 3rd edition, 2006.