Information

This information is part of the Modelica Standard Library maintained by the Modelica Association.

Restriction

This function shall be used within the restricted limits according to the referenced literature.

Reynolds number (for vena contraction) Re > 1e3 [Idelchik 2006, p. 222, diag. 4-15]
Relative length of vena contraction (L/d_hyd_0) > 0.015 [Idelchik 2006, p. 222, diag. 4-15]
Darcy friction factor lambda_FRI = 0.02 [Idelchik 2006, p. 222, sec. 4-15]

Geometry

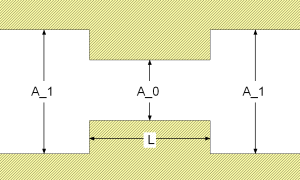
thickEdged

Calculation

The pressure loss dp for a thick edged orifice is determined by:

dp = zeta_TOT * (rho/2) * (velocity_1)^2

with

rho	as density of fluid [kg/m3],
velocity_1	as mean velocity in large cross sectional area [m/s],
zeta_TOT	as pressure loss coefficient [-].

The pressure loss coefficient zeta_TOT of a thick edged orifice can be calculated for different cross sectional areas A_0 and relative length of orifice l_bar = L/d_hyd_0 by:

zeta_TOT = (0.5*(1 - A_0/A_1)^0.75 + tau*(1 - A_0/A_1)^1.375 + (1 - A_0/A_1)^2 + lambda_FRI*l_bar)*(A_1/A_0)^2 [Idelchik 2006, p. 222, diag. 4-15]

with

A_0	cross sectional area of vena contraction [m2],
A_1	large cross sectional area of orifice [m2],
d_hyd_0	hydraulic diameter of vena contraction [m],
lambda_FRI	as constant Darcy friction factor [-],
l_bar	relative length of orifice [-],
L	length of vena contraction [m],
tau	geometry parameter [-].

The geometry factor tau is determined by [Idelchik 2006, p. 219, diag. 4-12]:

tau = (2.4 - l_bar)*10^(-phi)
phi = 0.25 + 0.535*l_bar^8 / (0.05 + l_bar^8) .

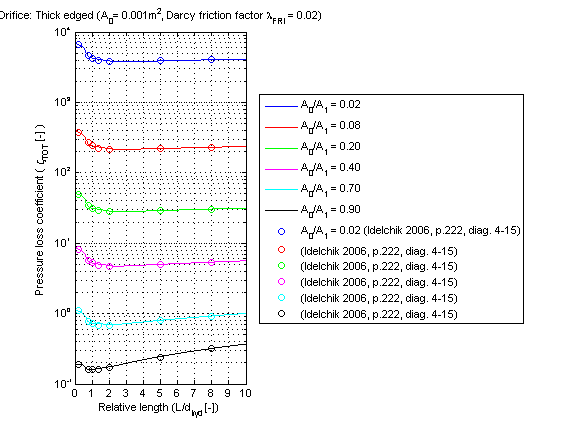
Verification

The pressure loss coefficient zeta_TOT of a thick edged orifice in dependence of a relative length (l_bar = L /d_hyd) with different ratios of cross sectional areas A_0/A_1 is shown in the figure below.

thickEdgedOverall_1

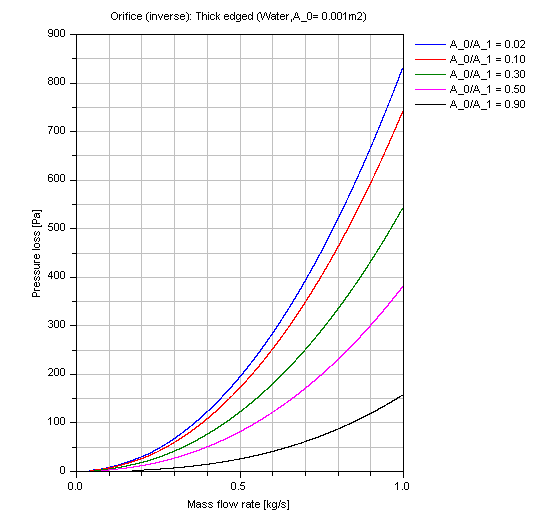
Incompressible case [Pressure loss = f(m_flow)]:

The pressure loss DP of an thick edged orifice in dependence of the mass flow rate m_flow of water for different ratios A_0/A_1 (where A_0 = 0.001 m^2) is shown in the figure below.

thickEdgedOverall_2

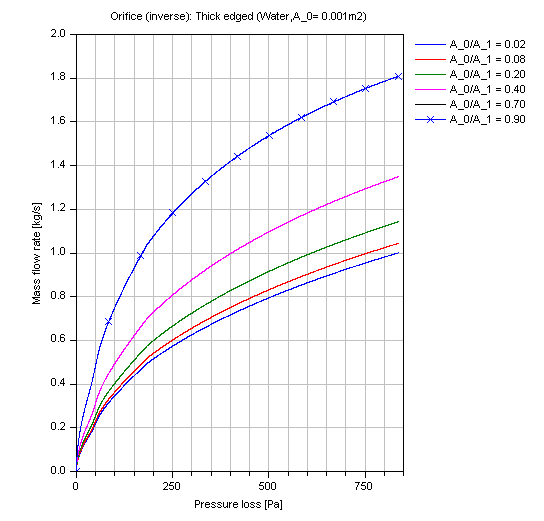
And for the compressible case [Mass flow rate = f(dp)]:

thickEdgedOverall_3

References

Elmqvist,H., M.Otter and S.E. Cellier:: Inline integration: A new mixed symbolic / numeric approach for solving differential-algebraic equation systems.. In Proceedings of European Simulation MultiConference, Prague, 1995.
Idelchik,I.E.:: Handbook of hydraulic resistance. Jaico Publishing House,Mumbai, 3rd edition, 2006.