Information

This information is part of the Modelica Standard Library maintained by the Modelica Association.

Calculation of pressure loss for a valve with different geometries at overall flow regime for incompressible and single-phase fluid flow in dependence of its opening.

Restriction

This function shall be used inside of the restricted limits according to the referenced literature.

developed fluid flow
ball valve
diaphragm valve
butterfly valve
gate valve
sluice valve

Geometry

Wide variations in valve geometry are possible and a manufacturer will not necessarily maintain geometric similarity between valves of the same type but of different size. Here pressure loss can be estimated for the following types of a valve:

ball valve
diaphragm valve
butterfly valve
gate valve
sluice valve

Calculation

The mass flow rate m_flow for valves out of pressure loss is determined by:

m_flow = [rho * dp * Av^2 / (zeta_TOT/2]^0.5
m_flow = (2/zeta_TOT)^0.5 * Av * (rho * dp)^0.5
m_flow = valveCharacteristic * Av * (rho * dp)^0.5

with

rho	as density of fluid [kg/m3],
Av	as (metric) flow coefficient (cross sectional area) [m^2],
m_flow	as mass flow rate [kg/s],
valveCharacteristic	as coefficient of a valve in dependence of its opening [-],
velocity	as mean velocity [m/s],
zeta_TOT	as pressure loss coefficient [-].

The valveCharacteristic is determined out of a correlation for the pressure loss coefficient (zeta_TOT) in dependence of its opening. The reason for introducing an additional variable valveCharacteristic is a different definition of the following pressure loss correlations of valves.

Verification

The pressure loss coefficient (zeta_TOT) of a valve with different geometries are shown in dependence of the opening in the figure below.

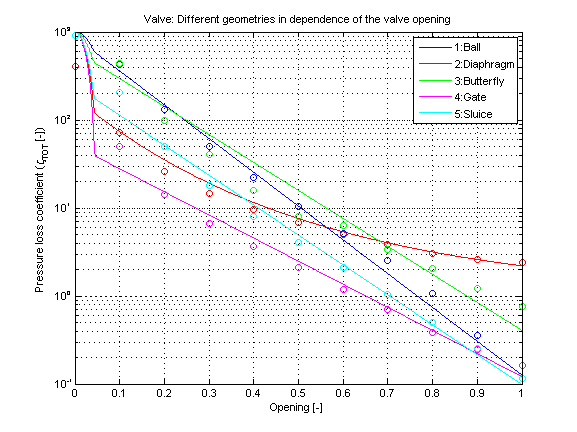
dp_severalGeometryOverall_z

Note that the pressure loss coefficients (zeta_TOT) are numerically optimized for very small openings (opening ≤ 5%). At openings smaller than 5% the pressure loss coefficient is smoothly set to a maximum value (zeta_TOT_max) to be adjusted as parameter. Therefore a very small leakage mass flow rate can be adjusted for a given pressure difference at almost closed valves. A very small leakage mass flow rate can often be neglected in system simulation with valves, whereas the numerical behaviour of the simulation is improved.

The mass flow rate of different valves at a constant opening of 50% in dependence of pressure loss is shown in the figure below.

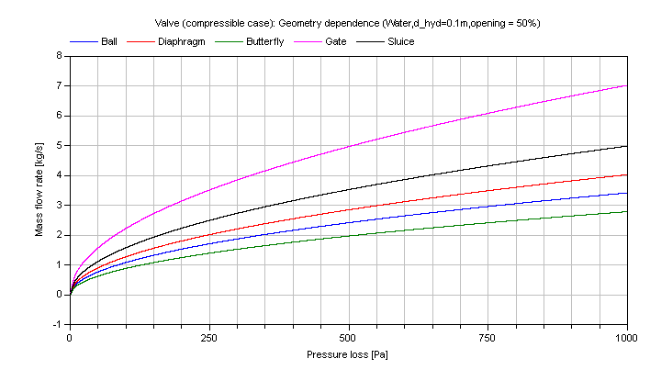
dp_severalGeometryOverall

References