WOLFRAM SYSTEM MODELER
dgelsx_vecComputes the minimum-norm solution to a real linear least squares problem with rank deficient A |
|
Wolfram Language
In[1]:=
SystemModel["Modelica.Math.Matrices.LAPACK.dgelsx_vec"]
Out[1]:=
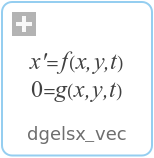
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Lapack documentation
Purpose
=======
This routine is deprecated and has been replaced by routine DGELSY.
DGELSX computes the minimum-norm solution to a real linear least
squares problem:
minimize || A * X - B ||
using a complete orthogonal factorization of A. A is an M-by-N
matrix which may be rank-deficient.
Several right hand side vectors b and solution vectors x can be
handled in a single call; they are stored as the columns of the
M-by-NRHS right hand side matrix B and the N-by-NRHS solution
matrix X.
The routine first computes a QR factorization with column pivoting:
A * P = Q * [ R11 R12 ]
[ 0 R22 ]
with R11 defined as the largest leading submatrix whose estimated
condition number is less than 1/RCOND. The order of R11, RANK,
is the effective rank of A.
Then, R22 is considered to be negligible, and R12 is annihilated
by orthogonal transformations from the right, arriving at the
complete orthogonal factorization:
A * P = Q * [ T11 0 ] * Z
[ 0 0 ]
The minimum-norm solution is then
X = P * Z' [ inv(T11)*Q1'*B ]
[ 0 ]
where Q1 consists of the first RANK columns of Q.
Arguments
=========
M (input) INTEGER
The number of rows of the matrix A. M >= 0.
N (input) INTEGER
The number of columns of the matrix A. N >= 0.
NRHS (input) INTEGER
The number of right hand sides, i.e., the number of
columns of matrices B and X. NRHS >= 0.
A (input/output) DOUBLE PRECISION array, dimension (LDA,N)
On entry, the M-by-N matrix A.
On exit, A has been overwritten by details of its
complete orthogonal factorization.
LDA (input) INTEGER
The leading dimension of the array A. LDA >= max(1,M).
B (input/output) DOUBLE PRECISION array, dimension (LDB,NRHS)
On entry, the M-by-NRHS right hand side matrix B.
On exit, the N-by-NRHS solution matrix X.
If m >= n and RANK = n, the residual sum-of-squares for
the solution in the i-th column is given by the sum of
squares of elements N+1:M in that column.
LDB (input) INTEGER
The leading dimension of the array B. LDB >= max(1,M,N).
JPVT (input/output) INTEGER array, dimension (N)
On entry, if JPVT(i) .ne. 0, the i-th column of A is an
initial column, otherwise it is a free column. Before
the QR factorization of A, all initial columns are
permuted to the leading positions; only the remaining
free columns are moved as a result of column pivoting
during the factorization.
On exit, if JPVT(i) = k, then the i-th column of A*P
was the k-th column of A.
RCOND (input) DOUBLE PRECISION
RCOND is used to determine the effective rank of A, which
is defined as the order of the largest leading triangular
submatrix R11 in the QR factorization with pivoting of A,
whose estimated condition number < 1/RCOND.
RANK (output) INTEGER
The effective rank of A, i.e., the order of the submatrix
R11. This is the same as the order of the submatrix T11
in the complete orthogonal factorization of A.
WORK (workspace) DOUBLE PRECISION array, dimension
(max( min(M,N)+3*N, 2*min(M,N)+NRHS )),
INFO (output) INTEGER
= 0: successful exit
< 0: if INFO = -i, the i-th argument had an illegal value
Syntax
(x, info, rank) = dgelsx_vec(A, b, rcond)
Inputs (3)
| A |
Type: Real[:,:] |
|---|---|
| b |
Type: Real[size(A, 1)] |
| rcond |
Default Value: 0.0 Type: Real Description: Reciprocal condition number to estimate rank |
Outputs (3)
| x |
Default Value: cat(1, b, zeros(max(nrow, ncol) - nrow)) Type: Real[max(size(A, 1), size(A, 2))] Description: solution is in first size(A,2) rows |
|---|---|
| info |
Type: Integer |
| rank |
Type: Integer Description: Effective rank of A |
