WOLFRAM SYSTEM MODELER
MatricesLibrary of functions operating on matrices |
|
Package Contents
|
Examples demonstrating the usage of the Math.Matrices functions |
|
|
Convert a matrix into its string representation |
|
|
Compare whether two Real matrices are identical |
|
|
Solve real system of linear equations A*x=b with a b vector (Gaussian elimination with partial pivoting) |
|
|
Solve real system of linear equations A*X=B with a B matrix (Gaussian elimination with partial pivoting) |
|
|
Solve linear equation A*x = b (exactly if possible, or otherwise in a least square sense; A may be non-square and may be rank deficient) |
|
|
Solve linear equation A*X = B (exactly if possible, or otherwise in a least square sense; A may be non-square and may be rank deficient) |
|
|
Solve a linear equality constrained least squares problem |
|
|
LU decomposition of square or rectangular matrix |
|
|
Solve real system of linear equations P*L*U*x=b with a b vector and an LU decomposition (from LU(..)) |
|
|
Solve real system of linear equations P*L*U*X=B with a B matrix and an LU decomposition (from LU(..)) |
|
|
Return eigenvalues and eigenvectors for a real, nonsymmetric matrix in a Real representation |
|
|
Return real valued block diagonal matrix J of eigenvalues of matrix A (A=V*J*Vinv) |
|
|
Return singular values and left and right singular vectors |
|
|
Return the QR decomposition of a square matrix with optional column pivoting (A(:,p) = Q*R) |
|
|
Return upper Hessenberg form of a matrix |
|
|
Return the real Schur form (rsf) S of a square matrix A, A=QZ*S*QZ' |
|
|
Return the Cholesky factorization of a symmetric positive definite matrix |
|
|
Return a balanced form of matrix A to improve the condition of A |
|
|
Return a balanced form of a system [A,B;C,0] to improve its condition by a state transformation |
|
|
Return the trace of matrix A, i.e., the sum of the diagonal elements |
|
|
Return determinant of a matrix (computed by LU decomposition; try to avoid det(..)) |
|
|
Return inverse of a matrix (try to avoid inv(..)) |
|
|
Return rank of a rectangular matrix (computed with singular values) |
|
|
Return the condition number norm(A)*norm(inv(A)) of a matrix A |
|
|
Return the reciprocal condition number of a matrix |
|
|
Return the p-norm of a matrix |
|
|
Return the Frobenius norm of a matrix |
|
|
Return the orthonormal nullspace of a matrix |
|
|
Return the exponential of a matrix by adaptive Taylor series expansion with scaling and balancing |
|
|
Return the exponential and the integral of the exponential of a matrix |
|
|
Return the exponential, the integral of the exponential, and time-weighted integral of the exponential of a matrix |
|
|
Return solution X of the continuous-time Lyapunov equation X*A + A'*X = C |
|
|
Return solution X of the continuous-time Sylvester equation A*X + X*B = C |
|
|
Return solution X of the continuous-time algebraic Riccati equation A'*X + X*A - X*B*inv(R)*B'*X + Q = 0 (care) |
|
|
Return solution X of the discrete-time Lyapunov equation A'*X*A + sgn*X = C |
|
|
Return solution of the discrete-time Sylvester equation A*X*B + sgn*X = C |
|
|
Return solution of discrete-time algebraic Riccati equation A'*X*A - X - A'*X*B*inv(R + B'*X*B)*B'*X*A + Q = 0 (dare) |
|
|
Sort the rows or columns of a matrix in ascending or descending order |
|
|
Flip the columns of a matrix in left/right direction |
|
|
Flip the rows of a matrix in up/down direction |
|
|
Interface to LAPACK library (should usually not directly be used but only indirectly via Modelica.Math.Matrices) |
|
|
Utility functions that should not be directly utilized by the user |
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Library content
This library provides functions operating on matrices. Below, the functions are ordered according to categories and a typical call of the respective function is shown. Most functions are solely an interface to the external LAPACK library.
Note: A' is a short hand notation of transpose(A):
Basic Information
- toString(A) - returns the string representation of matrix A.
- isEqual(M1, M2) - returns true if matrices M1 and M2 have the same size and the same elements.
Linear Equations
- solve(A,b) - returns solution x of the linear equation A*x=b (where b is a vector, and A is a square matrix that must be regular).
- solve2(A,B) - returns solution X of the linear equation A*X=B (where B is a matrix, and A is a square matrix that must be regular)
- leastSquares(A,b) - returns solution x of the linear equation A*x=b in a least squares sense (where b is a vector and A may be non-square and may be rank deficient)
- leastSquares2(A,B) - returns solution X of the linear equation A*X=B in a least squares sense (where B is a matrix and A may be non-square and may be rank deficient)
- equalityLeastSquares(A,a,B,b) - returns solution x of a linear equality constrained least squares problem: min|A*x-a|^2 subject to B*x=b
- (LU,p,info) = LU(A) - returns the LU decomposition with row pivoting of a rectangular matrix A.
- LU_solve(LU,p,b) - returns solution x of the linear equation L*U*x[p]=b with a b vector and an LU decomposition from "LU(..)".
- LU_solve2(LU,p,B) - returns solution X of the linear equation L*U*X[p,:]=B with a B matrix and an LU decomposition from "LU(..)".
Matrix Factorizations
- (eval,evec) = eigenValues(A) - returns eigen values "eval" and eigen vectors "evec" for a real, nonsymmetric matrix A in a Real representation.
- eigenValueMatrix(eval) - returns real valued block diagonal matrix of the eigenvalues "eval" of matrix A.
- (sigma,U,VT) = singularValues(A) - returns singular values "sigma" and left and right singular vectors U and VT of a rectangular matrix A.
- (Q,R,p) = QR(A) - returns the QR decomposition with column pivoting of a rectangular matrix A such that Q*R = A[:,p].
- (H,U) = hessenberg(A) - returns the upper Hessenberg form H and the orthogonal transformation matrix U of a square matrix A such that H = U'*A*U.
- realSchur(A) - returns the real Schur form of a square matrix A.
- cholesky(A) - returns the cholesky factor H of a real symmetric positive definite matrix A so that A = H'*H.
- (D,Aimproved) = balance(A) - returns an improved form Aimproved of a square matrix A that has a smaller condition as A, with Aimproved = inv(diagonal(D))*A*diagonal(D).
Matrix Properties
- trace(A) - returns the trace of square matrix A, i.e., the sum of the diagonal elements.
- det(A) - returns the determinant of square matrix A (using LU decomposition; try to avoid det(..))
- inv(A) - returns the inverse of square matrix A (try to avoid, use instead "solve2(..) with B=identity(..))
- rank(A) - returns the rank of square matrix A (computed with singular value decomposition)
- conditionNumber(A) - returns the condition number norm(A)*norm(inv(A)) of a square matrix A in the range 1..∞.
- rcond(A) - returns the reciprocal condition number 1/conditionNumber(A) of a square matrix A in the range 0..1.
- norm(A) - returns the 1-, 2-, or infinity-norm of matrix A.
- frobeniusNorm(A) - returns the Frobenius norm of matrix A.
- nullSpace(A) - returns the null space of matrix A.
Matrix Exponentials
- exp(A) - returns the exponential e^A of a matrix A by adaptive Taylor series expansion with scaling and balancing
- (phi, gamma) = integralExp(A,B) - returns the exponential phi=e^A and the integral gamma=integral(exp(A*t)*dt)*B as needed for a discretized system with zero order hold.
- (phi, gamma, gamma1) = integralExpT(A,B) - returns the exponential phi=e^A, the integral gamma=integral(exp(A*t)*dt)*B, and the time-weighted integral gamma1 = integral((T-t)*exp(A*t)*dt)*B as needed for a discretized system with first order hold.
Matrix Equations
- continuousLyapunov(A,C) - returns solution X of the continuous-time Lyapunov equation X*A + A'*X = C
- continuousSylvester(A,B,C) - returns solution X of the continuous-time Sylvester equation A*X + X*B = C
- continuousRiccati(A,B,R,Q) - returns solution X of the continuous-time algebraic Riccati equation A'*X + X*A - X*B*inv(R)*B'*X + Q = 0
- discreteLyapunov(A,C) - returns solution X of the discrete-time Lyapunov equation A'*X*A + sgn*X = C
- discreteSylvester(A,B,C) - returns solution X of the discrete-time Sylvester equation A*X*B + sgn*X = C
- discreteRiccati(A,B,R,Q) - returns solution X of the discrete-time algebraic Riccati equation A'*X*A - X - A'*X*B*inv(R + B'*X*B)*B'*X*A + Q = 0
Matrix Manipulation
- sort(M) - returns the sorted rows or columns of matrix M in ascending or descending order.
- flipLeftRight(M) - returns matrix M so that the columns of M are flipped in left/right direction.
- flipUpDown(M) - returns matrix M so that the rows of M are flipped in up/down direction.
See also
VectorsWolfram Language
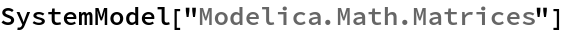
SystemModel["Modelica.Math.Matrices"]

