WOLFRAM SYSTEM MODELER
continuousRiccatiReturn solution X of the continuous-time algebraic Riccati equation A'*X + X*A - X*B*inv(R)*B'*X + Q = 0 (care) |
|
Wolfram Language
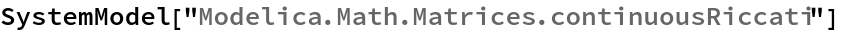
SystemModel["Modelica.Math.Matrices.continuousRiccati"]

Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Syntax
X = Matrices.continuousRiccati(A, B, R, Q);
(X, alphaReal, alphaImag) = Matrices.continuousRiccati(A, B, R, Q, true);
Description
Function continuousRiccati computes the solution X of the continuous-time algebraic Riccati equation
A'*X + X*A - X*G*X + Q = 0
with G = B*inv(R)*B'
using the Schur vector approach proposed by Laub [1].
It is assumed that Q is symmetric and positive semidefinite and R is symmetric, nonsingular and positive definite, (A,B) is stabilizable and (A,Q) is detectable.
These assumptions are not checked in this function !!
The assumptions guarantee that the Hamiltonian matrix
H = [A, -G; -Q, -A']
has no pure imaginary eigenvalue and can be put to an ordered real Schur form
U'*H*U = S = [S11, S12; 0, S22]
with orthogonal similarity transformation U. S is ordered in such a way, that S11 contains the n stable eigenvalues of the closed loop system with system matrix A - B*inv(R)*B'*X. If U is partitioned to
U = [U11, U12; U21, U22]
with dimensions according to S, the solution X is calculated by
X*U11 = U21.
With optional input refinement=true a subsequent iterative refinement based on Newton's method with exact line search is applied.
See continuousRiccatiIterative
for more information.
References
[1] Laub, A.J.
A Schur Method for Solving Algebraic Riccati equations.
IEEE Trans. Auto. Contr., AC-24, pp. 913-921, 1979.
Example
A = [0.0, 1.0;
0.0, 0.0];
B = [0.0;
1.0];
R = [1];
Q = [1.0, 0.0;
0.0, 2.0];
X = continuousRiccati(A, B, R, Q);
results in:
X = [2.0, 1.0;
1.0, 2.0];
See also
Matrices.Utilities.continuousRiccatiIterative, Matrices.discreteRiccati
Syntax
Inputs (5)
| A |
Type: Real[:,size(A, 1)] Description: Square matrix A in CARE |
|---|---|
| B |
Type: Real[size(A, 1),:] Description: Matrix B in CARE |
| R |
Default Value: identity(size(B, 2)) Type: Real[size(B, 2),size(B, 2)] Description: Matrix R in CARE |
| Q |
Default Value: identity(size(A, 1)) Type: Real[size(A, 1),size(A, 1)] Description: Matrix Q in CARE |
| refine |
Default Value: false Type: Boolean Description: True for subsequent refinement |
Outputs (3)
| X |
Type: Real[size(A, 1),size(A, 2)] Description: Stabilizing solution of CARE |
|---|---|
| alphaReal |
Type: Real[2 * size(A, 1)] Description: Real parts of eigenvalue=alphaReal+i*alphaImag |
| alphaImag |
Type: Real[2 * size(A, 1)] Description: Imaginary parts of eigenvalue=alphaReal+i*alphaImag |
Revisions
- 2010/05/31 by Marcus Baur, DLR-RM
