WOLFRAM SYSTEM MODELER
continuousLyapunovReturn solution X of the continuous-time Lyapunov equation X*A + A'*X = C |
|
Wolfram Language
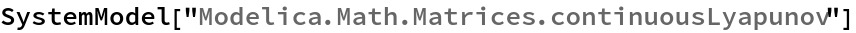
SystemModel["Modelica.Math.Matrices.continuousLyapunov"]

Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Syntax
X = Matrices.continuousLyapunov(A, C); X = Matrices.continuousLyapunov(A, C, ATisSchur, eps);
Description
This function computes the solution X of the continuous-time Lyapunov equation
X*A + A'*X = C
using the Schur method for Lyapunov equations proposed by Bartels and Stewart [1].
In a nutshell, the problem is reduced to the corresponding problem
Y*R' + R*Y = D
with R=U'*A'*U is the real Schur form of A' and D=U'*C*U and Y=U'*X*U
are the corresponding transformations of C and X. This problem is solved sequentially for the 1x1 or 2x2 Schur blocks by exploiting the block triangular form of R.
Finally the solution of the original problem is recovered as X=U*Y*U'.
The Boolean input "ATisSchur" indicates to omit the transformation to Schur in the case that A' has already Schur form.
References
[1] Bartels, R.H. and Stewart G.W.
Algorithm 432: Solution of the matrix equation AX + XB = C.
Comm. ACM., Vol. 15, pp. 820-826, 1972.
Example
A = [1, 2, 3, 4;
3, 4, 5, -2;
-1, 2, -3, -5;
0, 2, 0, 6];
C = [-2, 3, 1, 0;
-6, 8, 0, 1;
2, 3, 4, 5;
0, -2, 0, 0];
X = continuousLyapunov(A, C);
results in:
X = [1.633, -0.761, 0.575, -0.656;
-1.158, 1.216, 0.047, 0.343;
-1.066, -0.052, -0.916, 1.61;
-2.473, 0.717, -0.986, 1.48]
See also
Syntax
Inputs (4)
| A |
Type: Real[:,size(A, 1)] Description: Square matrix A in X*A + A'*X = C |
|---|---|
| C |
Type: Real[size(A, 1),size(A, 2)] Description: Square matrix C in X*A + A'*X = C |
| ATisSchur |
Default Value: false Type: Boolean Description: = true, if transpose(A) has already real Schur form |
| eps |
Default Value: Modelica.Math.Matrices.norm(A, 1) * 10 * 1e-15 Type: Real Description: Tolerance eps |
Outputs (1)
| X |
Type: Real[size(A, 1),size(A, 2)] Description: Solution X of the Lyapunov equation X*A + A'*X = C |
|---|
Revisions
- 2010/05/31 by Marcus Baur, DLR-RM
