WOLFRAM SYSTEM MODELER
continuousSylvesterReturn solution X of the continuous-time Sylvester equation A*X + X*B = C |
|
Wolfram Language
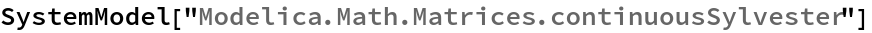
SystemModel["Modelica.Math.Matrices.continuousSylvester"]

Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Syntax
X = Matrices.continuousSylvester(A, B, C); X = Matrices.continuousSylvester(A, B, C, AisSchur, BisSchur);
Description
Function continuousSylvester computes the solution X of the continuous-time Sylvester equation
A*X + X*B = C.
using the Schur method for Sylvester equations proposed by Bartels and Stewart [1].
In a nutshell, the problem is reduced to the corresponding problem
S*Y + Y*T = D.
with S=U'*A*U is the real Schur of A, T=V'*T*V is the real Schur form of B and
D=U'*C*V and Y=U*X*V'
are the corresponding transformations of C and X. This problem is solved sequentially by exploiting the block triangular form of S and T.
Finally the solution of the original problem is recovered as X=U'*Y*V.
The Boolean inputs "AisSchur" and "BisSchur" indicate to omit one or both of the transformation to Schur in the case that A and/or B have already Schur form.
The function applies LAPACK-routine DTRSYL. See LAPACK.dtrsyl for more information.
References
[1] Bartels, R.H. and Stewart G.W.
Algorithm 432: Solution of the matrix equation AX + XB = C.
Comm. ACM., Vol. 15, pp. 820-826, 1972.
Example
A = [17.0, 24.0, 1.0, 8.0, 15.0 ;
23.0, 5.0, 7.0, 14.0, 16.0 ;
0.0, 6.0, 13.0, 20.0, 22.0;
0.0, 0.0, 19.0, 21.0, 3.0 ;
0.0, 0.0, 0.0, 2.0, 9.0];
B = [8.0, 1.0, 6.0;
0.0, 5.0, 7.0;
0.0, 9.0, 2.0];
C = [62.0, -12.0, 26.0;
59.0, -10.0, 31.0;
70.0, -6.0, 9.0;
35.0, 31.0, -7.0;
36.0, -15.0, 7.0];
X = continuousSylvester(A, B, C);
results in:
X = [0.0, 0.0, 1.0;
1.0, 0.0, 0.0;
0.0, 1.0, 0.0;
1.0, 1.0, -1.0;
2.0, -2.0, 1.0];
See also
Syntax
Inputs (5)
| A |
Type: Real[:,:] Description: Square matrix A |
|---|---|
| B |
Type: Real[:,:] Description: Square matrix B |
| C |
Type: Real[size(A, 1),size(B, 2)] Description: Matrix C |
| AisSchur |
Default Value: false Type: Boolean Description: = true, if A has already real Schur form |
| BisSchur |
Default Value: false Type: Boolean Description: = true, if B has already real Schur form |
Outputs (1)
| X |
Type: Real[size(A, 1),size(B, 2)] Description: Solution of the continuous Sylvester equation |
|---|
Revisions
- 2010/05/31 by Marcus Baur, DLR-RM
