WOLFRAM SYSTEM MODELER
LU_solveSolve real system of linear equations P*L*U*x=b with a b vector and an LU decomposition (from LU(..)) |
|
Wolfram Language
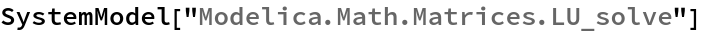
SystemModel["Modelica.Math.Matrices.LU_solve"]

Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Syntax
Matrices.LU_solve(LU, pivots, b);
Description
This function call returns the solution x of the linear systems of equations
P*L*U*x = b;
where P is a permutation matrix (implicitly
defined by vector pivots),
L is a lower triangular matrix with unit
diagonal elements (lower trapezoidal if m > n), and
U is an upper triangular matrix (upper trapezoidal if m < n).
The matrices of this decomposition are computed with function
Matrices.LU that
returns arguments LU and pivots
used as input arguments of Matrices.LU_solve.
With Matrices.LU and Matrices.LU_solve
it is possible to efficiently solve linear systems
with different right hand side vectors. If a linear system of equations with
just one right hand side vector shall be solved, it is
more convenient to just use the function
Matrices.solve.
If a unique solution x does not exist (since the LU decomposition is singular), an exception is raised.
The LU factorization is computed with the LAPACK function "dgetrf", i.e., by Gaussian elimination using partial pivoting with row interchanges. Vector "pivots" are the pivot indices, i.e., for 1 ≤ i ≤ min(m,n), row i of matrix A was interchanged with row pivots[i].
Example
Real A[3,3] = [1,2,3;
3,4,5;
2,1,4];
Real b1[3] = {10,22,12};
Real b2[3] = { 7,13,10};
Real LU[3,3];
Integer pivots[3];
Real x1[3];
Real x2[3];
algorithm
(LU, pivots) := Matrices.LU(A);
x1 := Matrices.LU_solve(LU, pivots, b1); // x1 = {3,2,1}
x2 := Matrices.LU_solve(LU, pivots, b2); // x2 = {1,0,2}
See also
Matrices.LU, Matrices.solve,Syntax
Inputs (3)
| LU |
Type: Real[:,size(LU, 1)] Description: L,U factors of Matrices.LU(..) for a square matrix |
|---|---|
| pivots |
Type: Integer[size(LU, 1)] Description: Pivots indices of Matrices.LU(..) |
| b |
Type: Real[size(LU, 1)] Description: Right hand side vector of P*L*U*x=b |
Outputs (1)
| x |
Type: Real[size(b, 1)] Description: Solution vector such that P*L*U*x = b |
|---|
