WOLFRAM SYSTEM MODELER

cholesky

Return the Cholesky factorization of a symmetric positive definite matrix

Wolfram Language

In[1]:=
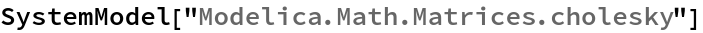
SystemModel["Modelica.Math.Matrices.cholesky"]
Out[1]:=

Information

This information is part of the Modelica Standard Library maintained by the Modelica Association.

Syntax

H = Matrices.cholesky(A);
H = Matrices.cholesky(A, upper=true);

Description

Function cholesky computes the Cholesky factorization of a real symmetric positive definite matrix A. The optional Boolean input "upper" specifies whether the upper or the lower triangular matrix is returned, i.e. 

A = H'*H   if upper is true (H is upper triangular)
A = H*H'   if upper is false (H is lower triangular)

The computation is performed by LAPACK.dpotrf.

Example

A  = [1, 0,  0;
      6, 5,  0;
      1, -2,  2];
S = A*transpose(A);

H = Matrices.cholesky(S);

results in:

H = [1.0,  6.0,  1.0;
     0.0,  5.0, -2.0;
     0.0,  0.0,  2.0]

with

transpose(H)*H = [1.0,  6.0,   1;
                  6.0, 61.0,  -4.0;
                  1.0, -4.0,   9.0] //=S

Syntax

H = cholesky(A, upper)

Inputs (2)

A

Type: Real[:,size(A, 1)]

Description: Symmetric positive definite matrix
upper

Default Value: true

Type: Boolean

Description: = true, if the right Cholesky factor (upper triangle) should be returned

Outputs (1)

H

Type: Real[size(A, 1),size(A, 2)]

Description: Cholesky factor U (upper=true) or L (upper=false) for A = U'*U or A = L*L'

Revisions

  • 2010/05/31 by Marcus Baur, DLR-RM