WOLFRAM SYSTEM MODELER
balanceABCReturn a balanced form of a system [A,B;C,0] to improve its condition by a state transformation |
|
Wolfram Language

SystemModel["Modelica.Math.Matrices.balanceABC"]
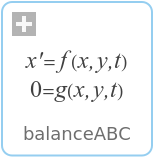
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Syntax
(scale,As,Bs,Cs) = Matrices.balanceABC(A,B,C); (scale,As,Bs) = Matrices.balanceABC(A,B); (scale,As,,Cs) = Matrices.balanceABC(A,C=C);
Description
This function returns a vector scale, such that with T=diagonal(scale) system matrix S_scale
|inv(T)*A*T, inv(T)*B|
S_scale = | |
| C*T, 0 |
has a better condition as system matrix S
|A, B|
S = | |
|C, 0|
that is, conditionNumber(S_scale) ≤ conditionNumber(S). The elements of vector scale are multiples of 2 which means that this function does not introduce round-off errors.
Balancing a linear dynamic system in state space form
der(x) = A*x + B*u
y = C*x + D*u
means to find a state transformation x_new = T*x = diagonal(scale)*x so that the transformed system is better suited for numerical algorithms.
Example
import Modelica.Math.Matrices;
A = [1, -10, 1000; 0.01, 0, 10; 0.005, -0.01, 10];
B = [100, 10; 1,0; -0.003, 1];
C = [-0.5, 1, 100];
(scale, As, Bs, Cs) := Matrices.balanceABC(A,B,C);
T = diagonal(scale);
Diff = [Matrices.inv(T)*A*T, Matrices.inv(T)*B;
C*T, zeros(1,2)] - [As, Bs; Cs, zeros(1,2)];
err = Matrices.norm(Diff);
-> Results in:
scale = {16, 1, 0.0625}
norm(A) = 1000.15, norm(B) = 100.504, norm(C) = 100.006
norm(As) = 10.8738, norm(Bs) = 16.0136, norm(Cs) = 10.2011
err = 0
The algorithm is taken from
- H. D. Joos, G. Grübel:
- RASP'91 Regulator Analysis and Synthesis Programs
DLR - Control Systems Group 1991
which is based on the balance function from EISPACK.
Syntax
Inputs (3)
| A |
Type: Real[:,size(A, 1)] Description: System matrix A |
|---|---|
| B |
Default Value: fill(0.0, size(A, 1), 0) Type: Real[size(A, 1),:] Description: System matrix B (need not be present) |
| C |
Default Value: fill(0.0, 0, size(A, 1)) Type: Real[:,size(A, 1)] Description: System matrix C (need not be present) |
Outputs (4)
| scale |
Type: Real[size(A, 1)] Description: diagonal(scale)=T is such that [inv(T)*A*T, inv(T)*B; C*T, 0] has smaller condition as [A,B;C,0] |
|---|---|
| As |
Type: Real[size(A, 1),size(A, 1)] Description: Balanced matrix A (= inv(T)*A*T ) |
| Bs |
Type: Real[size(A, 1),size(B, 2)] Description: Balanced matrix B (= inv(T)*B ) |
| Cs |
Type: Real[size(C, 1),size(A, 1)] Description: Balanced matrix C (= C*T ) |
Revisions
- Sept. 14, 2014 by Martin Otter: Implemented.
