WOLFRAM SYSTEM MODELER
nullSpaceReturn the orthonormal nullspace of a matrix |
|
Wolfram Language
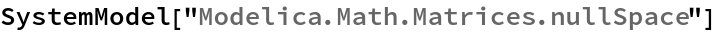
SystemModel["Modelica.Math.Matrices.nullSpace"]

Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Syntax
Z = Matrices.nullspace(A);
(Z, nullity) = Matrices.nullspace(A);
Description
This function calculates an orthonormal basis Z=[z_1, z_2, ...] of the nullspace of a matrix A, i.e., A*z_i=0.
The nullspace is obtained by SVD method. That is, matrix A is decomposed into the matrices S, U, V:
A = U*S*transpose(V)
with the orthonormal matrices U and V and the matrix S with
S = [S1, 0] S1 = [diag(s); 0]
and the singular values s={s1, s2, ..., sr} of A and r=rank(A). Note, that S has the same size as A. Since U and V are orthonormal we may write
transpose(U)*A*V = [S1, 0].
Matrix S1 obviously has full column rank and therefore, the left n-r rows (n is the number of columns of A or S) of matrix V span a nullspace of A.
The nullity of matrix A is the dimension of the nullspace of A. In view of the above, it becomes clear that nullity holds
nullity = n - r
with
n = number of columns of matrix A r = rank(A)
Example
A = [1, 2, 3, 1;
3, 4, 5, 2;
-1, 2, -3, 3];
(Z, nullity) = nullspace(A);
results in:
Z=[0.1715;
-0.686;
0.1715;
0.686]
nullity = 1
See also
Syntax
Inputs (1)
| A |
Type: Real[:,:] Description: Input matrix |
|---|
Outputs (2)
| Z |
Type: Real[size(A, 2),:] Description: Orthonormal nullspace of matrix A |
|---|---|
| nullity |
Type: Integer Description: Nullity, i.e., the dimension of the nullspace |
Revisions
- 2010/05/31 by Marcus Baur, DLR-RM
