WOLFRAM SYSTEM MODELER
balanceReturn a balanced form of matrix A to improve the condition of A |
|
Wolfram Language
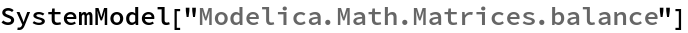
SystemModel["Modelica.Math.Matrices.balance"]

Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Syntax
(D,B) = Matrices.balance(A);
Description
This function returns a vector D, such that B=inv(diagonal(D))*A*diagonal(D) has a better condition as matrix A, i.e., conditionNumber(B) ≤ conditionNumber(A). The elements of D are multiples of 2 which means that this function does not introduce round-off errors. Balancing attempts to make the norm of each row of B equal to the norm of the respective column.
Balancing is used to minimize roundoff errors induced through large matrix calculations like Taylor-series approximation or computation of eigenvalues.
Example
- A = [1, 10, 1000; 0.01, 0, 10; 0.005, 0.01, 10]
- Matrices.norm(A, 1);
= 1020.0
- (T,B)=Matrices.balance(A)
- T
= {256, 16, 0.5}
- B
= [1, 0.625, 1.953125;
0.16, 0, 0.3125;
2.56, 0.32, 10.0]
- Matrices.norm(B, 1);
= 12.265625
The Algorithm is taken from
- H. D. Joos, G. Grübel:
- RASP'91 Regulator Analysis and Synthesis Programs
DLR - Control Systems Group 1991
which based on the balance function from EISPACK.
Syntax
Inputs (1)
| A |
Type: Real[:,size(A, 1)] |
|---|
Outputs (2)
| D |
Type: Real[size(A, 1)] Description: diagonal(D)=T is transformation matrix, such that B = inv(T)*A*T has smaller condition as A |
|---|---|
| B |
Type: Real[size(A, 1),size(A, 1)] Description: Balanced matrix (= inv(diagonal(D))*A*diagonal(D) ) |
Revisions
Release Notes
- July 5, 2002
by H. D. Joos and Nico Walther
Implemented.
