WOLFRAM SYSTEM MODELER
dlangeNorm of a matrix |
|
Wolfram Language
In[1]:=

SystemModel["Modelica.Math.Matrices.LAPACK.dlange"]
Out[1]:=
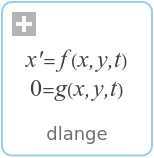
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Lapack documentation
Purpose
=======
DLANGE returns the value of the one norm, or the Frobenius norm, or
the infinity norm, or the element of largest absolute value of a
real matrix A.
Description
===========
DLANGE returns the value
DLANGE = ( max(abs(A(i,j))), NORM = 'M' or 'm'
(
( norm1(A), NORM = '1', 'O' or 'o'
(
( normI(A), NORM = 'I' or 'i'
(
( normF(A), NORM = 'F', 'f', 'E' or 'e'
where norm1 denotes the one norm of a matrix (maximum column sum),
normI denotes the infinity norm of a matrix (maximum row sum) and
normF denotes the Frobenius norm of a matrix (square root of sum of
squares). Note that max(abs(A(i,j))) is not a consistent matrix norm.
Arguments
=========
NORM (input) CHARACTER*1
Specifies the value to be returned in DLANGE as described
above.
M (input) INTEGER
The number of rows of the matrix A. M >= 0. When M = 0,
DLANGE is set to zero.
N (input) INTEGER
The number of columns of the matrix A. N >= 0. When N = 0,
DLANGE is set to zero.
A (input) DOUBLE PRECISION array, dimension (LDA,N)
The m by n matrix A.
LDA (input) INTEGER
The leading dimension of the array A. LDA >= max(M,1).
WORK (workspace) DOUBLE PRECISION array, dimension (MAX(1,LWORK)),
where LWORK >= M when NORM = 'I'; otherwise, WORK is not
referenced.
Syntax
anorm = dlange(A, norm)
Inputs (2)
| A |
Type: Real[:,:] Description: Real matrix A |
|---|---|
| norm |
Default Value: "1" Type: String Description: Specifies the norm, i.e., 1, I, F, M |
Outputs (1)
| anorm |
Type: Real Description: Norm of A |
|---|
