WOLFRAM SYSTEM MODELER
dorgqrGenerate a Real orthogonal matrix Q which is defined as the product of elementary reflectors as returned from dgeqrf |
|
Wolfram Language
In[1]:=

SystemModel["Modelica.Math.Matrices.LAPACK.dorgqr"]
Out[1]:=
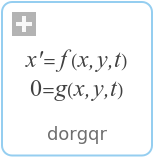
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Lapack documentation
Purpose
=======
DORGQR generates an M-by-N real matrix Q with orthonormal columns,
which is defined as the first N columns of a product of K elementary
reflectors of order M
Q = H(1) H(2) . . . H(k)
as returned by DGEQRF.
Arguments
=========
M (input) INTEGER
The number of rows of the matrix Q. M >= 0.
N (input) INTEGER
The number of columns of the matrix Q. M >= N >= 0.
K (input) INTEGER
The number of elementary reflectors whose product defines the
matrix Q. N >= K >= 0.
A (input/output) DOUBLE PRECISION array, dimension (LDA,N)
On entry, the i-th column must contain the vector which
defines the elementary reflector H(i), for i = 1,2,...,k, as
returned by DGEQRF in the first k columns of its array
argument A.
On exit, the M-by-N matrix Q.
LDA (input) INTEGER
The first dimension of the array A. LDA >= max(1,M).
TAU (input) DOUBLE PRECISION array, dimension (K)
TAU(i) must contain the scalar factor of the elementary
reflector H(i), as returned by DGEQRF.
WORK (workspace/output) DOUBLE PRECISION array, dimension (MAX(1,LWORK))
On exit, if INFO = 0, WORK(1) returns the optimal LWORK.
LWORK (input) INTEGER
The dimension of the array WORK. LWORK >= max(1,N).
For optimum performance LWORK >= N*NB, where NB is the
optimal blocksize.
If LWORK = -1, then a workspace query is assumed; the routine
only calculates the optimal size of the WORK array, returns
this value as the first entry of the WORK array, and no error
message related to LWORK is issued by XERBLA.
INFO (output) INTEGER
= 0: successful exit
< 0: if INFO = -i, the i-th argument has an illegal value
Syntax
(Q, info) = dorgqr(QR, tau)
Inputs (2)
| QR |
Type: Real[:,:] Description: QR from dgeqrf |
|---|---|
| tau |
Type: Real[min(size(QR, 1), size(QR, 2))] Description: The scalar factors of the elementary reflectors of Q |
Outputs (2)
| Q |
Default Value: QR Type: Real[size(QR, 1),size(QR, 2)] Description: Orthogonal matrix Q |
|---|---|
| info |
Type: Integer |
