WOLFRAM SYSTEM MODELER
OscillatorOscillator demonstrates the use of initial conditions |
|
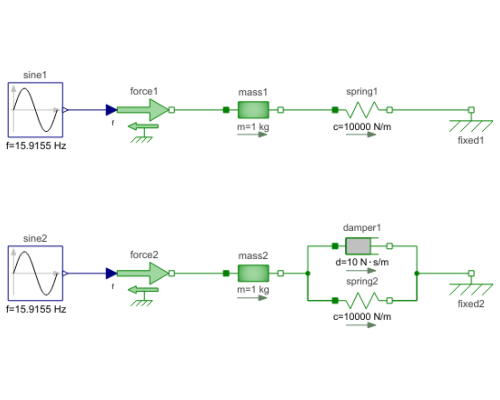
Diagram
Wolfram Language

SystemModel["Modelica.Mechanics.Translational.Examples.Oscillator"]
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
A spring - mass system is a mechanical oscillator. If no damping is included and the system is excited at resonance frequency infinite amplitudes will result. The resonant frequency is given by omega_res = sqrt(c / m) with:
c … spring stiffness and
m … mass.
To make sure that the system is initially at rest the initial conditions s(start=-0.5) and v(start=0) for the sliding masses are set. If damping is added the amplitudes are bounded.
Components (11)
| mass1 |
Type: Mass Description: Sliding mass with inertia |
|
|---|---|---|
| spring1 |
Type: Spring Description: Linear 1D translational spring |
|
| fixed1 |
Type: Fixed Description: Fixed flange |
|
| force1 |
Type: Force Description: External force acting on a drive train element as input signal |
|
| sine1 |
Type: Sine Description: Generate sine signal |
|
| mass2 |
Type: Mass Description: Sliding mass with inertia |
|
| spring2 |
Type: Spring Description: Linear 1D translational spring |
|
| fixed2 |
Type: Fixed Description: Fixed flange |
|
| force2 |
Type: Force Description: External force acting on a drive train element as input signal |
|
| sine2 |
Type: Sine Description: Generate sine signal |
|
| damper1 |
Type: Damper Description: Linear 1D translational damper |