ARCHProcess

ARCHProcess[κ,{α1,…,αq}]

represents an autoregressive conditionally heteroscedastic process of order q, driven by a standard white noise.

ARCHProcess[κ,{α1,…,αq},init]

represents an ARCH process with initial data init.

Details

  • ARCHProcess is a discrete-time and continuous-state random process.
  • A process x[t] is an ARCH process if the conditional mean Expectation[x[t] {x[t-1], …}]=0 and the conditional variance 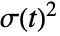given by Expectation [x[t]2{x[t-1, …}] satisfies the equation .
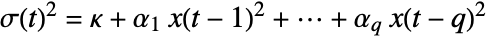  • The initial data init can be given as a list 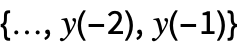{...,y(-2),y(-1)} or a single path TemporalData object with time stamps understood as {...,-2,-1}.
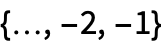  • A scalar ARCH process can have non-negative coefficients αi and a positive coefficient κ.
  • ARCHProcess[q] represents an ARCH process of order q for use in EstimatedProcess and related functions.
  • ARCHProcess can be used with such functions as RandomFunction, CovarianceFunction, and TimeSeriesForecast.

Examples

open allclose all

Basic Examples  (3)

Simulate an ARCHProcess:

Unconditional mean and variance of a weakly stationary process:

With fixed initial values:

The observations are uncorrelated but dependent:

The squared values of the data are correlated:

Scope  (13)

Basic Examples  (8)

Simulate an ensemble of paths:

Simulate with arbitrary precision:

Simulate a weakly stationary process with given initial values:

A non-weakly stationary process:

An integrated ARCHProcess:

Explosive ARCHProcess:

Such a process is not second-order stationary:

Conditions for an ARCHProcess to be covariance stationary:

Region of second-order stationarity for an ARCHProcess[2]:

Estimate an ARCHProcess:

Use maximum conditional likelihood estimator:

Forecast:

Find the forecast 20 steps ahead:

Find mean squared errors of the forecast:

The forecasted states are equal to zero, hence the forecasted standard deviation bounds are as follows:

Plot the values with mean squared errors:

Process Slice Properties  (5)

Moments of a weakly stationary ARCH of order 1:

Moment of an ARCH process with given initial conditions:

Skewness:

Kurtosis:

Region where kurtosis is defined:

Simulate slice distribution:

Probability density function of the sample:

Use Monte Carlo method to calculate NProbability for slice distribution:

Calculate NExpectation:

Compare to the second Moment:

Properties & Relations  (3)

The values of an ARCHProcess are uncorrelated:

Corresponding ARProcess:

For a process with given initial values:

Squared values of an ARCHProcess follow an ARProcess:

CorrelationFunction and PartialCorrelationFunction of squared values:

The corresponding autoregressive process:

CorrelationFunction and PartialCorrelationFunction of the AR process:

Wolfram Research (2014), ARCHProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/ARCHProcess.html.

Text

Wolfram Research (2014), ARCHProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/ARCHProcess.html.

CMS

Wolfram Language. 2014. "ARCHProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ARCHProcess.html.

APA

Wolfram Language. (2014). ARCHProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ARCHProcess.html

BibTeX

@misc{reference.wolfram_2024_archprocess, author="Wolfram Research", title="{ARCHProcess}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ARCHProcess.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_archprocess, organization={Wolfram Research}, title={ARCHProcess}, year={2014}, url={https://reference.wolfram.com/language/ref/ARCHProcess.html}, note=[Accessed: 21-November-2024 ]}