Ball

Ball[p]

represents the unit ball centered at the point p.

Ball[p,r]

represents the ball of radius r centered at the point p.

Ball[{p1,p2,…},r]

represents a collection of balls of radius r.

Details and Options

  • Ball is also known as center interval, disk, ball, and hyperball.
  • Ball can be used as a geometric region and a graphics primitive.
  • Ball[] is equivalent to Ball[{0,0,0}].
  • Ball[n] for integer n is equivalent to Ball[{0,…,0}], a unit ball in .
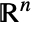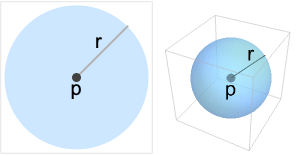
  • Ball represents a filled ball {x|TemplateBox[{{x, -, p}}, Norm]<=r}. The region is 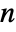dimensional for point p of length .
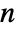  • Ball allows p to be any point in 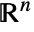and r any positive real number.
  • Ball can be used in Graphics and Graphics3D.
  • In graphics, the points p, pi and radii r can be Scaled and Dynamic expressions.
  • Graphics rendering is affected by directives such as FaceForm, EdgeForm, Specularity, Opacity, and color.
  • Ball[{p1,p2,…},{r1,r2,…}] represents a collection of spheres with centers pi and radii ri.

Background & Context

  • Ball is a graphics and geometry primitive that represents a ball in 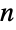-dimensional space. In particular, Ball[p,r] represents a (filled-in) ball {x:TemplateBox[{{x, -, p}}, Norm]<=r} in TemplateBox[{}, Reals]^n with center p and radius r, where r may be any non-negative real number and p can have any positive length 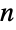. The shorthand form Ball[p] is equivalent to Ball[p,1] and Ball[n] is equivalent to Ball[ConstantArray[0, n],1], while Ball[] autoevaluates to Ball[{0,0,0}].
  • Collections of ball objects (multi-balls) of common radius 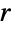may be efficiently represented using Ball[{p1,…,pk},r] and balls of varying radii represented using Ball[{p1,…,pk},{r1,…,rk}].
  • Ball objects can be visually formatted in two and three dimensions using Graphics and Graphics3D, respectively. The appearance of Ball objects in graphics can be modified by specifying the edge directive EdgeForm (in 2D) or face directive FaceForm (in 3D), color directives such as Red, the transparency and specularity directives Opacity and Specularity, and the style option Antialiasing.
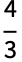
  • Ball may also serve as a region specification over which a computation should be performed. For example, Integrate[1,{x,y,z}∈Ball[{0,0,0},r]] and Volume[Ball[{0,0,0},r]] both return the volume 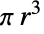of a 3D ball of radius .
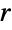  • Ball is related to a number of other symbols. Sphere represents the boundary of a ball, as can be computed using RegionBoundary[Ball[{x,y,z},r]]. Ball is a generalization of Interval and Disk to arbitrary dimension, and Ellipsoid is a generalization of Ball in the sense that Ball[{p1,…,pk},1] is equivalent to Ellipsoid[{p1,…,pk},ConstantArray[1,k]] for all 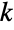. SphericalShell gives a filled shell obtained by removing a small ball from the interior of a larger concentric ball. Ball objects in 3D may be represented as ImplicitRegion[(x-u)2+(y-v)2+(z-w)2≤r2,{u,v,w}] or ParametricRegion[a{Cos[θ]Sin[ϕ],Sin[θ]Sin[ϕ],Cos[ϕ]}-{x,y,z},{{θ,0,2π},{ϕ,0,π},{a,0,r}]. Precomputed properties of the 3D ball and its variants in standard position are available using SolidData["entity", "property"] or EntityValue[Entity["Ball","entity"],"property"], where "entity" is one of "Ball" or "HalfBall".

Examples

open allclose all

Basic Examples  (2)

A unit ball in 3D:

In 2D:

Volume and centroid:

Scope  (22)

Graphics  (12)

Specification  (4)

The default is a unit ball at the origin in 3D:

Unit balls in different dimensions:

Balls with different positions and radii:

Multiple balls with equal radii:

Styling  (4)

Balls with different specular exponents:

Black ball that glows red:

Opacity specifies the face opacity:

2D styling:

Coordinates  (4)

Specify coordinates by fractions of the plot range:

Specify radius by fractions of the plot range:

Specify scaled offsets from the ordinary coordinates:

Points can be Dynamic:

Regions  (10)

Embedding dimension is the dimension of the space in which the ball lives:

Geometric dimension is the dimension of the shape itself:

Membership testing:

Get conditions for point membership:

Volume:

Centroid:

Distance from a point:

The distance to the nearest point for a 2D ball:

The equidistance contours for a 3D ball:

Signed distance from a point:

Signed distance to a 2D ball:

Nearest point in the region:

Nearest points to an enclosing sphere:

A ball is bounded:

Find its range:

Integrate over a ball region:

Optimize over a ball region:

Solve equations in a ball region:

Applications  (3)

Find the minimum surface area for a ball with volume :

Total mass for a ball region with density given by :

Find the mass of caffeine in a ball with a radius of 3 centimeters:

Density of caffeine:

Volume of ball:

Mass of caffeine in the ball:

Properties & Relations  (5)

Disk is a special case of Ball:

Sphere is the RegionBoundary of Ball:

Ellipsoid is a generalization of Ball:

ImplicitRegion can represent any Ball:

Ball is a norm ball for the Euclidean norm:

Neat Examples  (1)

Random ball collections:

Wolfram Research (2014), Ball, Wolfram Language function, https://reference.wolfram.com/language/ref/Ball.html.

Text

Wolfram Research (2014), Ball, Wolfram Language function, https://reference.wolfram.com/language/ref/Ball.html.

CMS

Wolfram Language. 2014. "Ball." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Ball.html.

APA

Wolfram Language. (2014). Ball. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Ball.html

BibTeX

@misc{reference.wolfram_2024_ball, author="Wolfram Research", title="{Ball}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Ball.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ball, organization={Wolfram Research}, title={Ball}, year={2014}, url={https://reference.wolfram.com/language/ref/Ball.html}, note=[Accessed: 21-November-2024 ]}