BiweightLocation
BiweightLocation[list]
gives the value of the biweight location estimator of the elements in list.
BiweightLocation[list,c]
gives the value of the biweight location estimator with scaling parameter c.
Details and Options
- BiweightLocation is a robust location estimator.
- BiweightLocation is given by a weighted mean of the elements. Elements farther from the center have lower weights.
- The width scale of the weight function is controlled by a parameter c. Larger c indicates more data values are included in the computation of the statistic, and vice versa.
- For the list {x1,x2,…,xn}, the value of the biweight location estimator is given by
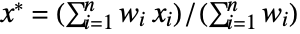, where 
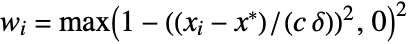and 
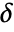is Median[{x1-x*,x2-x*,…,xn-x*}]. The value x* of the estimator is computed iteratively, with the initial value chosen automatically by default. - BiweightLocation[list] is equivalent to BiweightLocation[list,6].
- BiweightLocation[{{x1,y1,…},{x2,y2,…},…}] gives {BiweightLocation[{x1,x2,…}],BiweightLocation[{y1,y2,…}],…}.
- BiweightLocation allows c to be any positive real number.
- The following options can be given:
-
AccuracyGoal Automatic the accuracy sought MaxIterations Automatic maximum number of iterations to use Method Automatic method to use PrecisionGoal Automatic the precision sought WorkingPrecision MachinePrecision the precision used in internal computations - The setting Method{"InitialPoint"x0} allows for a custom initial value
.
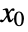Examples
open allclose allBasic Examples (4)
BiweightLocation of a list:
BiweightLocation of columns of a matrix:
BiweightLocation of a list with scaling parameter 7:
BiweightLocation of a list of dates:
Scope (8)
Same inputs with different precisions:
Biweight location with different scaling parameters:
Biweight location for a matrix gives columnwise estimate:
Biweight location of a large array:
Find a biweight location of a TimeSeries:
The biweight location depends only on the values:
Biweight location works with data involving quantities:
Compute biweight location of dates:
Options (2)
MaxIterations (1)
The value of BiweightLocation is computed iteratively. Limit the number of iterations attempted in the computation:
Method (1)
Adjust the starting value in the computation of BiweightLocation:
Limit the number of iterations with a better starting value:
Applications (3)
Obtain a robust estimate of location when outliers are present:
Extreme values have a large influence on the Mean:
Consider data from a Gaussian mixture distribution:
Estimate the center with Mean:
The sample mean estimator has a large spread for non-Gaussian data. The standard deviation of the estimator is:
Estimate the center with BiweightLocation:
Use bootstrapping to assess the spread of the biweight location estimator:
Simulate a trajectory with heavy-tailed measurement noise:
The underlying signal and simulated path with noise:
Smooth the trajectory using a moving BiweightLocation:
Properties & Relations (3)
Compute the biweight location of a sample:
Values outside of the interval 
have no effect on the statistic. Here 
is the value of biweight location and 
is the median absolute deviation with respect to 
. 
is a scaling parameter with default value equal to 6:
The shape of the weight function w(x) being used in computing biweight location:
Multiply the smallest and the largest values in the sample by 2 and compute the biweight location again:
For normally distributed samples, BiweightLocation and Mean are nearly the same:
For non-normally distributed samples such as data from CauchyDistribution, BiweightLocation gives a better estimate of the center location than Mean:
BiweightLocation approaches Mean for large values of c:
Text
Wolfram Research (2017), BiweightLocation, Wolfram Language function, https://reference.wolfram.com/language/ref/BiweightLocation.html (updated 2024).
CMS
Wolfram Language. 2017. "BiweightLocation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/BiweightLocation.html.
APA
Wolfram Language. (2017). BiweightLocation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BiweightLocation.html