CauchyDistribution
CauchyDistribution[a,b]
represents a Cauchy distribution with location parameter a and scale parameter b.
represents a Cauchy distribution with location parameter 0 and scale parameter 1.
Details
- CauchyDistribution is also known as a Lorentz or Breit–Wigner distribution.
- The probability density for value
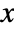in a Cauchy distribution is proportional to 
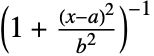. » - CauchyDistribution allows a to be any real number and b to be any positive real number.
- CauchyDistribution allows a and b to be any quantities of the same unit dimensions. »
- CauchyDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- CauchyDistribution[a,b] represents a continuous statistical distribution defined over the set of real numbers and parametrized by two values a and b, where a is a real-valued "location parameter" and b is a positive "scale parameter". The probability density function (PDF) of a Cauchy distribution is continuous, unimodal, and symmetric about the point
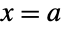. The height and width of the PDF vary according to the parameter b, with values of b nearer to zero corresponding to PDFs that are taller and steeper. In addition, the tails of the PDF are "fat" in the sense that the PDF decreases algebraically rather than decreasing exponentially for large values 
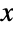. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Cauchy distribution is sometimes called the Lorentz distribution or the Breit–Wigner distribution. - Study of what is now called the Cauchy distribution dates back to the work of Pierre de Fermat in the seventeenth century. It had already provided a rich, colorful contribution to existing probability theory by the time it became associated with Augustin-Louis Cauchy in the 1850s—some century and a half after its genesis. Originally, the Cauchy distribution was studied as a novelty that served as a counterexample to a number of generally accepted results and concepts of the day. Today, it is an established distribution in its own right and one with a number of applications across a variety of fields of study. For example, the Cauchy distribution shares a natural link with Brownian motion of certain molecules and is the distribution that describes the energy profile of a resonance in nonrelativistic contexts. The Cauchy distribution can also be used to model a number of phenomena in areas such as risk analysis, mechanical and electrical theory, and physical anthropology.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Cauchy distribution. Distributed[x,CauchyDistribution[a,b]], written more concisely as xCauchyDistribution[a,b], can be used to assert that a random variable x is distributed according to a Cauchy distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[CauchyDistribution[a,b],x] and CDF[CauchyDistribution[a,b],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. Note that because of the fat tails of the Cauchy distribution, some of these quantities may fail to exist.
- DistributionFitTest can be used to test if a given dataset is consistent with a Cauchy distribution, EstimatedDistribution to estimate a Cauchy parametric distribution from given data, and FindDistributionParameters to fit data to a Cauchy distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Cauchy distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Cauchy distribution.
- TransformedDistribution can be used to represent a transformed Cauchy distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Cauchy distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Cauchy distributions.
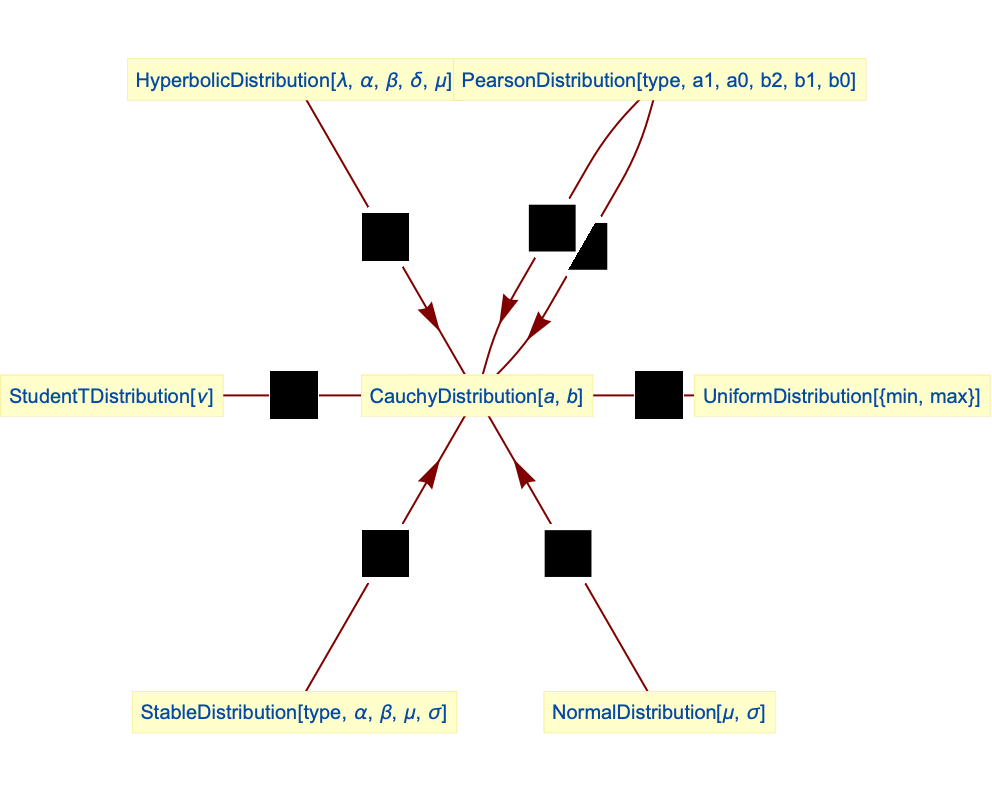
- The Cauchy distribution is related to a number of other distributions. For example, CauchyDistribution[0,1] has precisely the same PDF as StudentTDistribution[1]. CauchyDistribution can also be viewed as a transformation of both NormalDistribution and UniformDistribution by way of TransformedDistribution, and is a limiting case of both PearsonDistribution and HyperbolicDistribution in the sense that the PDFs of PearsonDistribution[4,1,-a,(1+ϵ)/2,-a,(a2+b2)/2] as ϵ tends to zero (for
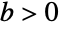) and of HyperbolicDistribution[-1/2, α, 0, δ, μ] as α tends to zero are precisely the same as the PDFs of CauchyDistribution[a, b] and CauchyDistribution[μ, δ], respectively. CauchyDistribution is also related to PearsonDistribution, ParetoDistribution, and StableDistribution.
Examples
open allclose allBasic Examples (4)
Scope (6)
Generate a sample of pseudorandom numbers from a Cauchy distribution:
Compare the histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
Higher-order moments are indeterminate:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (1)
A pendulum hangs at height 
above the origin. The angle 
that it makes with the vertical axis is uniformly distributed from 
to 
. Find the distribution of the horizontal distance 
between the pendulum and the vertical axis [MathWorld]:
And this is CauchyDistribution, as shown:
Find the probability that the distance between the pendulum and vertical axis is at least 
:
Assume 
and find the area under the PDF plot equal to this probability:
Properties & Relations (13)
Cauchy distribution is closed under translation and scaling by a positive factor:
Cauchy distribution is closed under certain transformations:
Sum of Cauchy-distributed variates follows Cauchy distribution:
Proof based on characteristic functions:
The inverse of a Cauchy distribution centered at 0 is also a Cauchy distribution:
Relationships to other distributions:
CauchyDistribution[0,1] is equivalent to StudentTDistribution with 
:
The ratio of two normally distributed variables is a CauchyDistribution:
If 
is uniformly distributed, then 
has a CauchyDistribution:
Cauchy distribution is a limiting case of a PearsonDistribution of type 4:
CauchyDistribution is a special case of a PearsonDistribution of type 7:
Cauchy distribution is a StableDistribution:
CauchyDistribution is a singular limit of a HyperbolicDistribution of 
, given 
and 
:
LogLikelihood function of CauchyDistribution may have multiple local maxima:
Find extrema of the likelihood function:
Select likelihood's maxima and find the corresponding values:
Visualize the likelihood as a function of location parameter 
:
Possible Issues (2)
CauchyDistribution is not defined when a is nonreal:
CauchyDistribution is not defined when b is non-positive:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Text
Wolfram Research (2007), CauchyDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/CauchyDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "CauchyDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/CauchyDistribution.html.
APA
Wolfram Language. (2007). CauchyDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CauchyDistribution.html