CensoredDistribution
CensoredDistribution[{xmin,xmax},dist]
represents the distribution of values that come from dist and are censored to be between xmin and xmax.
CensoredDistribution[{{xmin,xmax},{ymin,ymax},…},dist]
represents the distribution of values that come from the multivariate distribution dist and are censored to be between xmin and xmax, ymin and ymax, etc.
Details

- CensoredDistribution[{xmin,xmax},dist] is equivalent to TransformedDistribution[f,xdist], where f is given by Piecewise[{{xmin,x<=xmin},{x,xmin<x<xmax},{xmax,x>=xmax}}].
- Common cases for {xmin,xmax} include:
-
{-∞,xmax} censoring from above, right-censoring {xmin,∞} censoring from below, left-censoring {xmin,xmax} doubly censored, interval-censoring {-∞,∞},None no censoring, uncensored - CensoredDistribution can be used with such functions as Mean, CDF, RandomVariate, etc.
Background & Context
- CensoredDistribution[{xmin,xmax},dist] represents a statistical distribution modeling data that is known to be taken from the univariate distribution dist for all
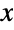 in the interval
in the interval 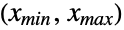 and that is assumed to be constantly equal to
and that is assumed to be constantly equal to 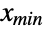 (respectively, constantly equal to
(respectively, constantly equal to 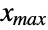 ) for
) for 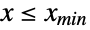 (respectively for
(respectively for 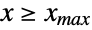 ). The terms uncensored, left-censored, right-censored, and doubly censored are used to describe univariate censorings for which {xmin,xmax} has the form {-∞,∞}, {xmin,∞}, {-∞,xmax}, and {xmin,xmax}, respectively, while univariate dist may be either continuous (e.g. NormalDistribution, GammaDistribution, or BetaDistribution) or discrete (e.g. PoissonDistribution, BinomialDistribution, or BernoulliDistribution) and may be defined in terms of transformations, censoring, or truncations (by way of TransformedDistribution, CensoredDistribution, and TruncatedDistribution, respectively) of known distributions.
). The terms uncensored, left-censored, right-censored, and doubly censored are used to describe univariate censorings for which {xmin,xmax} has the form {-∞,∞}, {xmin,∞}, {-∞,xmax}, and {xmin,xmax}, respectively, while univariate dist may be either continuous (e.g. NormalDistribution, GammaDistribution, or BetaDistribution) or discrete (e.g. PoissonDistribution, BinomialDistribution, or BernoulliDistribution) and may be defined in terms of transformations, censoring, or truncations (by way of TransformedDistribution, CensoredDistribution, and TruncatedDistribution, respectively) of known distributions. - The multivariate CensoredDistribution[{{
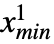 ,
,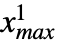 },{
},{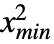 ,
,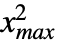 },… ,{
},… ,{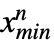 ,
,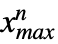 }},dist] is defined analogously and thus represents the distribution of vectors
}},dist] is defined analogously and thus represents the distribution of vectors 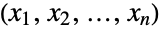 taken from the multivariate distribution dist and whose
taken from the multivariate distribution dist and whose 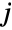
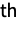 component
component 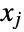 is censored to be in the interval
is censored to be in the interval 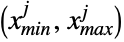 . As in the univariate case, multivariate dist may again be either continuous (e.g. MultinormalDistribution) or discrete (e.g. MultivariateHypergeometricDistribution), and may also be defined as a copula or product (using CopulaDistribution and ProductDistribution, respectively) of known distributions.
. As in the univariate case, multivariate dist may again be either continuous (e.g. MultinormalDistribution) or discrete (e.g. MultivariateHypergeometricDistribution), and may also be defined as a copula or product (using CopulaDistribution and ProductDistribution, respectively) of known distributions. - Censored distributions arise when modeling data for which the values are only partially known (i.e. those datasets containing only partially observed or accuracy-constrained data), and the analysis of datasets containing censored values dates back to the eighteenth-century smallpox investigations of Daniel Bernoulli. The existence of such data is relatively common in fields such as medicine and physiology, as well as in reliability and manufacturing, where failure predictions must sometimes be made without having observed actual failure. Censored distributions are also commonly utilized tools in survival analysis, and a variety of specialized statistical tools (e.g. censored regression) exists to analyze such datasets.
- By definition, CensoredDistribution[{xmin,xmax},dist] is equivalent to TransformedDistribution[f,xdist], where f is given by Piecewise[{{xmin,x<=xmin},{x,xmin<x<xmax},{xmax,x>=xmax}}]. CensoredDistribution is often confused with TruncatedDistribution, though the two are fundamentally different in the sense that censoring puts the probability at the end of the censoring interval, while the probability is distributed over the truncation interval via truncation.
Examples
open allclose allBasic Examples (2)
Scope (26)
Basic Uses (9)
Define different types of censoring for a univariate discrete distribution:
Define different types of censoring for a univariate continuous distribution:
Define a right-censored discrete distribution:
Compare probability density functions:
Find probability at 9 for the censored distribution:
Compare to the probability of obtaining a value of at least 9 for the original distribution:
Censor a continuous distribution:
Use a histogram and plot the original density function to visualize the point probability:
A distribution censored to one point:
Censoring for a multivariate continuous distribution:
Compute the expectation of an expression for this distribution:
Censoring for a multivariate discrete distribution:
Compute the mean for the distribution:
Compare with the result obtained using a random sample drawn from the distribution:
Define a doubly censored distribution:
Cumulative distribution function:
The mean and variance of the censored distribution:
Moment has closed form for symbolic order:
Parametric Distributions (5)
Define a right-censored continuous distribution:
Cumulative distribution function:
Plot a histogram for a random sample. The spike corresponds to the DiracDelta part of PDF:
Define a censored GeometricDistribution:
Compare probability density functions:
The values of the PDF at the censoring points are equal to the following probabilities:
Define a doubly censored GammaDistribution:
Define a right-censored PoissonDistribution:
Compare HazardFunction:
Define a two-dimensional censored DirichletDistribution:
Nonparametric Distributions (3)
Define a censored EmpiricalDistribution:
Compare cumulative distribution functions:
Define a censored HistogramDistribution:
Define a censored SmoothKernelDistribution:
Derived Distributions (9)
Define a censored ParameterMixtureDistribution:
Cumulative distribution function:
Define a censored MixtureDistribution:
Cumulative distribution function:
Define a a censored OrderDistribution:
Define a censored CensoredDistribution:
Compare to doubly censored Poisson distribution:
Define a censored TruncatedDistribution:
Compare cumulative distribution functions:
Define a censored TransformedDistribution:
Cumulative distribution function:
Define a censored MarginalDistribution:
Compare with the PDF of the marginal:
Define a censored ProductDistribution:
Visualize the density function using a random sample:
Censoring of a QuantityDistribution evaluates to QuantityDistribution:
Applications (4)
An insurance company buys reinsurance at retention level ![]() . Assuming claims follow lognormal distribution, find moments of insurer's payout random variate:
. Assuming claims follow lognormal distribution, find moments of insurer's payout random variate:
Find moments of reinsurer's payout random variate:
The lifetime of a component follows a RayleighDistribution. The components are tested for failures for ![]() hours, and if a component has not failed, it is assumed to have a lifetime of exactly
hours, and if a component has not failed, it is assumed to have a lifetime of exactly ![]() hours. Find the length of the test so that at most 5% of the tested components have a lifetime longer than
hours. Find the length of the test so that at most 5% of the tested components have a lifetime longer than ![]() :
:
Find the test lifetime distribution for ![]() :
:
Compare the censored distribution with the actual lifetime distribution:
Compare the average lifetimes:
The number of shots a beginner golf player needs to sink a 4-par hole follows a PoissonDistribution with an average of 9 shots. Assuming that on the golf course he picks up the ball after the tenth shot, find the distribution of the number of shots on a 4-par hole:
The average number of shots per 4-par hole on the golf course:
Find the probability that he needs more than 4 shots to sink the ball:
The body weight of adult males in the US follows a normal distribution with a mean of 191 lbs and a standard deviation of 70 lbs. Assuming that each bathroom scale has an upper limit of 300 lbs, find the weight distribution when the measurements are done with a generic bathroom scale:
Cumulative distribution function:
Visualize the density function with a random sample:
Find the probability of weighing at least 200 lbs:
Properties & Relations (4)
CensoredDistribution is a special case of TransformedDistribution:
Compare censoring with truncating for a discrete distribution:
While censoring, the weight from outside is placed at the ends of the censoring interval:
While truncating, the weight from outside is evenly distributed over the truncation interval:
Compare censoring and truncating of a continuous distribution:
While censoring, the probability is put at the end of the censoring interval:
While truncating, the probability is distributed over the truncation interval:
Censoring of a continuous distribution may result in a mixed distribution, which is neither continuous nor discrete:
The CDF for the mixed type censored distribution is discontinuous at censoring points:
Visualize the cumulative distribution function:
The probability density function for a censored distribution is not defined, and PDF returns unevaluated:
Differentiation of the CDF results in a function that does not integrate to one:
The sample probability density estimators do not converge as the sample size increases:
Compare this with histograms for the underlying continuous distribution, where estimators do converge:
Possible Issues (1)
Censoring of a continuous distribution may result in a mixed distribution, which is neither continuous nor discrete:
The PDF for the mixed type censored distribution is not defined: »
Computations with mixed type distributions are fully supported. Compute special moments:
Estimate a censored distribution:
Mixed type distribution can be interpreted as mixture of a continuous and discrete distributions:
Text
Wolfram Research (2010), CensoredDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/CensoredDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "CensoredDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/CensoredDistribution.html.
APA
Wolfram Language. (2010). CensoredDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CensoredDistribution.html