represents a Bernoulli distribution with probability parameter p.


BernoulliDistribution
represents a Bernoulli distribution with probability parameter p.
Details
- BernoulliDistribution is also known as the coin toss distribution or Bernoulli trial.
- BernoulliDistribution gives value
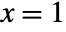 with probability
with probability 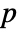 , and
, and 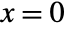 with probability
with probability 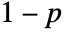 . »
. » - BernoulliDistribution allows probability parameter p to be a dimensionless quantity. »
- BernoulliDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- BernoulliDistribution[p] represents a discrete statistical distribution defined on the real numbers, where the parameter p is represents a probability parameter satisfying
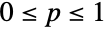 . The Bernoulli distribution is sometimes referred to as the coin toss distribution or as the distribution of a Bernoulli trial. It has a discrete probability density function (PDF) that returns the value p at
. The Bernoulli distribution is sometimes referred to as the coin toss distribution or as the distribution of a Bernoulli trial. It has a discrete probability density function (PDF) that returns the value p at 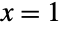 , gives
, gives 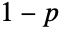 at
at 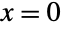 , and evaluates to 0 for all other real numbers.
, and evaluates to 0 for all other real numbers. - The Bernoulli distribution is named for Swiss mathematician Jacob Bernoulli and is designed to model the simple action of flipping a (fair or unfair) coin. Traditionally, p is thought of as the probability with which the experiment "succeeds" (so that 1 represents a successful experiment), whereas
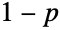 is the probability of "failure" (so that 0 represents a failed experiment). In the coin flip analogy, 1 typically represents heads, while tails is represented by 0. The value
is the probability of "failure" (so that 0 represents a failed experiment). In the coin flip analogy, 1 typically represents heads, while tails is represented by 0. The value 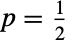 corresponds to flipping a fair coin. Despite being defined very simply, the Bernoulli distribution serves as the basis for a number of other, often more complicated mathematical concepts including the Bernoulli sequence in probability, the Bernoulli measure in measure theory, and the Bernoulli scheme in dynamical systems. Within the study of stochastic processes, the Bernoulli distribution is also the motivation behind the so-called Bernoulli process (BernoulliProcess), a discrete-time stochastic process consisting of a (finite or infinite) sequence of random variables, each of which is independent and identically Bernoulli distributed. Moreover, many real-world scenarios showing a well-defined dichotomy of independent outcome possibilities can be modeled as Bernoulli processes. Examples include the probability of rolling a particular value with a single (fair) die and the numbers of defective products, given a defect rate that is independent of the production scale.
corresponds to flipping a fair coin. Despite being defined very simply, the Bernoulli distribution serves as the basis for a number of other, often more complicated mathematical concepts including the Bernoulli sequence in probability, the Bernoulli measure in measure theory, and the Bernoulli scheme in dynamical systems. Within the study of stochastic processes, the Bernoulli distribution is also the motivation behind the so-called Bernoulli process (BernoulliProcess), a discrete-time stochastic process consisting of a (finite or infinite) sequence of random variables, each of which is independent and identically Bernoulli distributed. Moreover, many real-world scenarios showing a well-defined dichotomy of independent outcome possibilities can be modeled as Bernoulli processes. Examples include the probability of rolling a particular value with a single (fair) die and the numbers of defective products, given a defect rate that is independent of the production scale. - RandomVariate can be used to give one or more machine- or arbitrary-precision pseudorandom variates from a Bernoulli distribution. Distributed[x,BernoulliDistribution[p]], written more concisely as xBernoulliDistribution[p], can be used to assert that a random variable x is distributed according to a Bernoulli distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[BernoulliDistribution[p],x] and CDF[BernoulliDistribution[p],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
- DistributionFitTest can be used to test if a given dataset is consistent with a Bernoulli distribution, EstimatedDistribution to estimate a Bernoulli parametric distribution from given data, and FindDistributionParameters to fit data to a Bernoulli distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Bernoulli distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Bernoulli distribution.
- TransformedDistribution can be used to represent a transformed Bernoulli distribution and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Bernoulli distribution and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Bernoulli distributions.
- BernoulliDistribution is related to a number of other probability distributions. For example, BernoulliDistribution[p] is equivalent to a single instance of BinomialDistribution[1,p], i.e. PDF[BernoulliDistribution[p],k] is identical to Piecewise[Table[{PDF[BinomialDistribution[1,p],l],kl},{l,0,1}]]. Similarly, the sum of n independent Bernoulli variables with common success rate p is modeled by BinomialDistribution[n,p]. In addition, a number of naturally occurring quantities emerging from collections of independent Bernoulli-distributed random variables may be modeled according to other well-known distributions. For example, the number of successes in the first n data points distributed according to BernoulliDistribution[p] has distribution BinomialDistribution[n,p] while the number of trials to get one (respectively r) successes has distribution GeometricDistribution[p] (respectively NegativeBinomialDistribution[r,p]).
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a Bernoulli distribution:
Compare the frequency of 1 in the sample with the probability of getting 1:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
The distribution is symmetric for ![]() :
:
Find where the kurtosis attains its minimum:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Use dimensionless Quantity to define BernoulliDistribution:
Applications (6)
Simulate a sequence of fair coin tosses:
The probability of throwing a 6 on a six-sided die can be modeled as a Bernoulli distribution:
Simulate throwing a die, if you are only interested in sixes:
Out of 10 bulbs produced, one is defective. Simulate production of 100 bulbs:
Find the number of good bulbs in the batch:
Find the expected number of good bulbs per batch of 100:
Find the probability that a randomly selected bulb is good:
A lottery sells 10 tickets for $1 per ticket. Each time there is only one winning ticket. A gambler has $5 to spend. Find his probability of winning if he buys 5 tickets in 5 different lotteries:
His probability of winning is greater if he buys 5 tickets in the same lottery:
Simulate a symmetric random walk with values -1 and 1:
In an optical communication system, transmitted light generates current at the receiver. The number of electrons follows the parametric mixture of Poisson distribution and another distribution, depending on the type of light. If the source uses coherent laser light of intensity ![]() , then the electron count distribution is Poisson:
, then the electron count distribution is Poisson:
Which is PoissonDistribution:
If the source uses thermal illumination, then the Poisson parameter follows ExponentialDistribution with parameter ![]() and the electron count distribution is:
and the electron count distribution is:
These two distributions are distinguishable and allow the type of source to be determined:
Properties & Relations (4)
The probability of getting anything other than zero and one is zero:
Relationships to other distributions:

BernoulliDistribution is equivalent to BinomialDistribution of one trial:
BinomialDistribution is the sum of ![]() independent Bernoulli variables:
independent Bernoulli variables:
Possible Issues (2)
BernoulliDistribution is not defined when p is not between zero and one:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Tech Notes
Text
Wolfram Research (2007), BernoulliDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/BernoulliDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "BernoulliDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BernoulliDistribution.html.
APA
Wolfram Language. (2007). BernoulliDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BernoulliDistribution.html
BibTeX
@misc{reference.wolfram_2025_bernoullidistribution, author="Wolfram Research", title="{BernoulliDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/BernoulliDistribution.html}", note=[Accessed: 02-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_bernoullidistribution, organization={Wolfram Research}, title={BernoulliDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/BernoulliDistribution.html}, note=[Accessed: 02-January-2026]}