ExponentialDistribution
represents an exponential distribution with scale inversely proportional to parameter λ.
Details
- The probability density for value
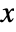 in an exponential distribution is proportional to
in an exponential distribution is proportional to 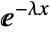 for
for 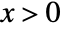 , and is zero for
, and is zero for 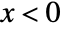 . »
. » - ExponentialDistribution allows λ to be any positive real number.
- ExponentialDistribution allows λ to be a quantity of any unit dimension. »
- ExponentialDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- ExponentialDistribution[λ] represents a continuous statistical distribution defined over the interval
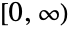 and parametrized by a positive real number λ. The probability density function (PDF) of an exponential distribution is monotonically decreasing. In addition, the tails of the PDF are "thin", in the sense that the PDF decreases exponentially for large values of
and parametrized by a positive real number λ. The probability density function (PDF) of an exponential distribution is monotonically decreasing. In addition, the tails of the PDF are "thin", in the sense that the PDF decreases exponentially for large values of 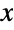 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The exponential distribution is sometimes referred to as the negative exponential distribution, the one-parameter exponential distribution, or the antilogarithmic distribution.
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The exponential distribution is sometimes referred to as the negative exponential distribution, the one-parameter exponential distribution, or the antilogarithmic distribution. - Historically, the exponential distribution has been used most widely to describe events recurring "at random in time", i.e. in circumstances for which the future lifetime of an individual has the same distribution regardless of its present state. Use of the exponential distribution has increased significantly over the last 75 years, due in part to considerable research within the field of order statistics beginning in the early to mid-1950s. Since then, the exponential distribution has been used to model various phenomena over intervals of approximately constant rate, e.g. the number of phone calls placed in a specific time interval each day. In stochastic processes, the exponential distribution describes the lengths of interarrival times in homogeneous Poisson processes (i.e. continuous-time counting processes whose increments are independent, stationary, and Poisson-distributed—implemented as PoissonProcess). The exponential distribution is also used in credit risk modeling, queueing theory, reliability theory, physics, and hydrology.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from an exponential distribution. Distributed[x,ExponentialDistribution[λ]], written more concisely as xExponentialDistribution[λ], can be used to assert that a random variable x is distributed according to an exponential distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[ExponentialDistribution[λ],x] and CDF[ExponentialDistribution[λ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with an exponential distribution, EstimatedDistribution to estimate an exponential parametric distribution from given data, and FindDistributionParameters to fit data to an exponential distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic exponential distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic exponential distribution.
- TransformedDistribution can be used to represent a transformed exponential distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain an exponential distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving exponential distributions.
- The exponential distribution is related to a large number of other distributions. Its occurrence relative to a PoissonProcess induces a relationship with PoissonDistribution and CompoundPoissonDistribution. ExponentialDistribution can be thought of as a basis for the extreme value distributions family, due to the fact that ExponentialDistribution[1] can be transformed into each of ExtremeValueDistribution, GumbelDistribution, FrechetDistribution, and WeibullDistribution, while ExponentialDistribution can be obtained from each of GammaDistribution, LaplaceDistribution, BenktanderWeibullDistribution, LogisticDistribution, ParetoDistribution, PearsonDistribution, PowerDistribution, and RayleighDistribution by way of TransformedDistribution and/or TruncatedDistribution. Several distributions can be derived by combining various other distributions with ExponentialDistribution, e.g. GeometricDistribution (by combining ExponentialDistribution with PoissonDistribution), KDistribution (by combining with GammaDistribution), HoytDistribution (by combining with ArcSinDistribution), and ParetoDistribution (by combining with either ErlangDistribution or GammaDistribution).
Examples
open allclose allBasic Examples (4)
Scope (7)
Generate a sample of pseudorandom numbers from an exponential distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness and kurtosis are constant:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Closed form for symbolic order:
Hazard function of exponential distribution is constant and depends on the parameter λ:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (9)
A battery has a lifespan that is exponentially distributed with rate parameter ![]() per hour. Find the probability that a random battery has a lifespan of less than 2500 hours:
per hour. Find the probability that a random battery has a lifespan of less than 2500 hours:
Compute directly using the CDF:
A relay has an exponentially distributed lifetime with a failure rate of ![]() failures per year. In order to estimate warranty costs, estimate the number of relays out of 10000 that will fail in the first six months of use. The failure rate is also known as the hazard rate:
failures per year. In order to estimate warranty costs, estimate the number of relays out of 10000 that will fail in the first six months of use. The failure rate is also known as the hazard rate:
Hence the lifetime distribution (in years) for relays is:
The probability of failure within the first six months:
The expected number of failures within the first six months in the batch of 10000 relays:
A product has a time to failure that is exponentially distributed with parameter ![]() . Find the product's reliability at 1, 2, and 3 years. Reliability is another name for SurvivalFunction:
. Find the product's reliability at 1, 2, and 3 years. Reliability is another name for SurvivalFunction:
Suppose the lifetime of an appliance has an exponential distribution with average lifetime of 10 years. Find the appliance lifetime distribution:
Find the probability that a used appliance with ![]() years of use will not fail in the next 5 years:
years of use will not fail in the next 5 years:
Using the memoryless property of ExponentialDistribution:
Assume the waiting time a customer spends in a restaurant is exponentially distributed with an average wait time of 5 minutes. Find the probability that the customer will have to wait more than 10 minutes:
Find the probability that the customer has to wait an additional 10 minutes, given that he or she has already been waiting for at least 10 minutes (the past does not matter):
The data contains waiting times in days between serious (magnitude at least 7.5 or over 1000 fatalities) earthquakes worldwide, recorded from 12/16/1902 to 3/4/1977:
Fit ExponentialDistribution to the data:
Compare the histogram of the data with the PDF of the estimated distribution:
Find the average number of days between major earthquakes:
Find the probability that two serious earthquakes occur within 100 days:
Simulate times between the next 30 serious earthquakes occurring worldwide:
Waiting times at a receiver for signals coming from four independent transmitters are exponentially distributed with parameters ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , respectively. Find the probability that the signal from the third transmitter arrives first to the receiver:
, respectively. Find the probability that the signal from the third transmitter arrives first to the receiver:
Find the distribution of the waiting time for any signal at the receiver:
Find the average waiting time for any signal at the receiver:
Simulate the waiting time between signals arriving at the receiver for ![]() ,
, ![]() ,
, ![]() , and
, and ![]() :
:
A system is composed of 4 independent components, each with lifespan exponentially distributed with parameter ![]() per hour. Find the probability that no component fails before 500 hours:
per hour. Find the probability that no component fails before 500 hours:
Directly use SurvivalFunction:
Find the probability that exactly one component will fail in the first 1200 hours:
Directly use CDF and SurvivalFunction:
By using BooleanCountingFunction, you can also define the logical condition:
In an optical communication system, transmitted light generates current at the receiver. The number of electrons follows the parametric mixture of Poisson distribution and other distributions, depending on the type of light. If the source uses coherent laser light of intensity λ, then the electron count distribution is Poisson:
Which is PoissonDistribution:
If the source uses thermal illumination, then the Poisson parameter follows ExponentialDistribution with parameter ![]() and the electron count distribution is:
and the electron count distribution is:
These two distributions are distinguishable and allow the type of source to be determined:
Properties & Relations (31)
Exponential distribution is closed under scaling by a positive factor:
The variance is the square of the mean:
The minimum of exponential distributions is exponentially distributed:
The minimum of ![]() identically distributed variables:
identically distributed variables:
The exponential distribution is memoryless (the past does not matter):
Relationships to other distributions:
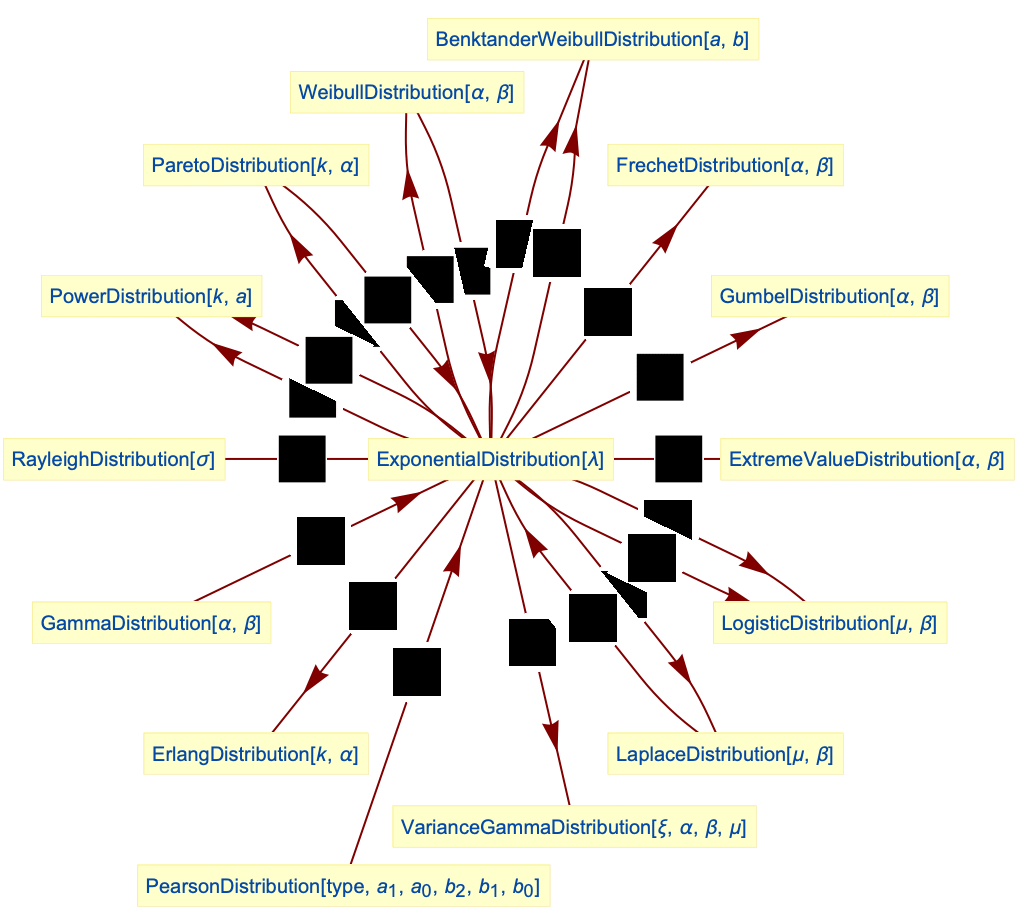
BenktanderWeibullDistribution reduces to a truncated ExponentialDistribution:
Shifted ExponentialDistribution is a BenktanderWeibullDistribution:
Exponential distribution is a limit of a scaled BetaDistribution:
PowerDistribution is a transformation of an exponential distribution:
Exponential distribution can be obtained from PowerDistribution:
Exponential distribution can be obtained from BetaDistribution:
Sum of independent exponentially distributed random variables follows ErlangDistribution:
For an arbitrary number of variables:
ExponentialDistribution[1] can be transformed into an extreme value distributions family:
ExponentialDistribution is a special case of WeibullDistribution:
ExponentialDistribution is a special case of GammaDistribution:
The difference of two variates from the same exponential distribution follows LaplaceDistribution:
The difference of two different exponential distributions follows VarianceGammaDistribution:
Exponential distribution is a transformation of LaplaceDistribution:
LogisticDistribution is a transformation from exponential distribution:
LogisticDistribution is a transformation of exponential distribution:
ParetoDistribution is a transformation of exponential distribution:
Transformation of a ParetoDistribution yields an exponential distribution:
Exponential distribution is a special case of type 3 PearsonDistribution:
PowerDistribution is a transformation of exponential distribution:
Exponential distribution can be obtained from RayleighDistribution:
Exponential distribution is the limiting distribution of the ![]() where
where ![]() has UniformDistribution:
has UniformDistribution:
The parametric mixture of PoissonDistribution and exponential distribution follows GeometricDistribution:
KDistribution can be obtained from ExponentialDistribution and GammaDistribution:
HoytDistribution can be obtained from ExponentialDistribution and ArcSinDistribution:
ParetoDistribution can be obtained as a quotient of ExponentialDistribution and ErlangDistribution:
ParetoDistribution can be obtained as a quotient of ExponentialDistribution and GammaDistribution:
Possible Issues (2)
ExponentialDistribution is not defined when λ is not a positive real number:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Text
Wolfram Research (2007), ExponentialDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ExponentialDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "ExponentialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ExponentialDistribution.html.
APA
Wolfram Language. (2007). ExponentialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ExponentialDistribution.html