ExtremeValueDistribution

ExtremeValueDistribution[α,β]

represents an extreme value distribution with location parameter α and scale parameter β.

ExtremeValueDistribution[]

represents an extreme value distribution with location parameter 0 and scale parameter 1.

Details

  • The extreme value distribution gives the asymptotic distribution of the maximum value in a sample from a distribution such as the normal distribution.
  • The probability density for value 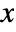in an extreme value distribution is proportional to . »
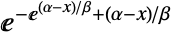  • The asymptotic distribution of the minimum value, also sometimes called an extreme value distribution, is implemented in the Wolfram Language as GumbelDistribution. »
  • ExtremeValueDistribution allows α to be any real number and β to be any positive real number.
  • ExtremeValueDistribution allows α and β to be any quantities of the same unit dimensions. »
  • ExtremeValueDistribution can be used with such functions as Mean, CDF, and RandomVariate. »

Background & Context

  • ExtremeValueDistribution[α,β] represents a continuous statistical distribution defined over the set of real numbers and parametrized by a real number α, called a "location parameter", and a positive real number β, called a "scale parameter". While the overall behavior of the probability density function (PDF) of the extreme value distribution is smooth and unimodal, the parameters α and β determine the horizontal location and overall height and steepness, respectively, of the PDF. In addition, the tails of the PDF are "thin", in the sense that the PDF decreases exponentially for large values of 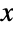. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The extreme value distribution may also be referred to as the type-1 extreme value distribution, the doubly exponential distribution (not to be confused with LaplaceDistribution, which may also be called doubly exponential), the log-Weibull distribution (WeibullDistribution), or the Gumbel-type distribution (not to be confused with GumbelDistribution).
  • While ExtremeValueDistribution is sometimes referred to as "the" extreme value distribution, it is actually one of four distributions (along with GumbelDistribution, FrechetDistribution, and WeibullDistribution) classified under the general heading "extreme value distribution". The extreme value distribution is obtained as the limiting distribution of greatest values in random samples of increasing size, and because its PDF is doubly exponential (i.e. is of the form Exp[-Exp[…]]), the graph of the distribution has more exaggerated features (like higher peaks and thinner tails), a property unique among distributions. It was introduced in the early 1920s to address the need in astronomy to utilize or reject outlying observations. A cornerstone in the field known as extreme value theory, the extreme value distribution is widely utilized to describe situations that are "extremely unlikely" (i.e. those in which datasets consist of variates with extreme deviations from the median), e.g. extreme floods, catastrophic insurance losses, and large wildfires. Moreover, the extreme value distribution can be used in biology as a tool to model evolutionary genetic mutations.
  • RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from an extreme value distribution. Distributed[x,ExtremeValueDistribution[α,β]], written more concisely as xExtremeValueDistribution[α,β], can be used to assert that a random variable x is distributed according to an extreme value distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
  • The probability density and cumulative distribution functions may be given using PDF[ExtremeValueDistribution[α,β],x] and CDF[ExtremeValueDistribution[α,β],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
  • DistributionFitTest can be used to test if a given dataset is consistent with an extreme value distribution, EstimatedDistribution to estimate an extreme value parametric distribution from given data, and FindDistributionParameters to fit data to an extreme value distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic extreme value distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic extreme value distribution.
  • TransformedDistribution can be used to represent a transformed extreme value distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain an extreme value distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving extreme value distributions.
  • The extreme value distribution is related to a number of other distributions. As mentioned previously, ExtremeValueDistribution is one of a number of distributions, including GumbelDistribution, FrechetDistribution, and WeibullDistribution, that are used to describe extremely unlikely events. This qualitative relationship also has quantitative components, as the PDF of ExtremeValueDistribution[α,β] is precisely the same as that of TransformedDistribution[-u,u GumbelDistribution[-α,β]] and TransformedDistribution[-β α Log[u/β]+α,u WeibullDistribution[α,β]]. ExtremeValueDistribution is a transformation of ExponentialDistribution and MinStableDistribution, and is a special case of MaxStableDistribution, in the sense that the PDF of ExtremeValueDistribution[α,β] is identical to that of MaxStableDistribution[α,β,0]. ExtremeValueDistribution is also related to ExpGammaDistribution, ExponentialDistribution, and LogisticDistribution.

Examples

open allclose all

Basic Examples  (4)

Probability density function:

Cumulative distribution function:

Mean and variance:

Median:

Scope  (7)

Generate a sample of pseudorandom numbers from an extreme value distribution:

Compare the histogram to the PDF:

Distribution parameters estimation:

Estimate the distribution parameters from sample data:

Compare a density histogram of the sample with the PDF of the estimated distribution:

Skewness and kurtosis are constant:

Different moments with closed forms as functions of parameters:

Moment:

CentralMoment:

FactorialMoment:

Cumulant:

Closed form for symbolic order:

Hazard function:

Quantile function:

Consistent use of Quantity in parameters yields QuantityDistribution:

Find the median and the quartile deviation of the oil price:

Applications  (3)

The lifetime of a device has an extreme value distribution. Find the reliability of the device:

The failure rate has a horizontal asymptote that depends only on the second parameter:

Find the reliability of two such devices in series:

Find the reliability of two such devices in parallel:

Compare the reliability of both systems for and :

ExtremeValueDistribution can be used to model monthly maximum wind speeds. Recorded monthly maxima of wind speeds in km/h for Boston, MA, from January 1950 till December 2009:

Fit the distribution to the data:

Compare the histogram of the data with the PDF of the estimated distribution:

Find the probability of monthly maximum wind speed exceeding 60 mph:

Find the average monthly maximum wind speed:

Simulate maximum wind speed for 30 months:

Construct an approximation for the distribution of maximum value in a normal sample of size :

Compare density function plots:

Mean of the approximation:

Compare with the mean of exact distribution:

Properties & Relations  (16)

Extreme value distribution is closed under translation and scaling by a positive factor:

Skewness is the negative of the skewness of GumbelDistribution:

ExtremeValueDistribution is skewed to the right, while GumbelDistribution is skewed to the left:

Kurtosis is the same as for GumbelDistribution:

ExtremeValueDistribution is closed under taking Max:

CDF of ExtremeValueDistribution solves the stability postulate equation:

Find the conditions on and such that the above is an identity:

Relationships to other distributions:

ExtremeValueDistribution is the negative of GumbelDistribution:

ExtremeValueDistribution is a transformation of WeibullDistribution:

WeibullDistribution is a transformation of extreme value distribution:

Extreme value distribution is a special case of MaxStableDistribution:

Extreme value distribution is a transformation of MinStableDistribution:

Extreme value distribution is a transformation of ExponentialDistribution:

The difference of two variates from extreme value distribution follows the same distribution as the difference of two variates from GumbelDistribution, which is LogisticDistribution:

The sum of extreme value distribution and GumbelDistribution follows LogisticDistribution:

LogisticDistribution is a ParameterMixtureDistribution of extreme value distribution:

The maximum of ExponentialDistribution and ExtremeValueDistribution follows ShiftedGompertzDistribution:

Possible Issues  (3)

The distribution of maximum values is given by ExtremeValueDistribution:

The distribution of minimum values is given by GumbelDistribution:

ExtremeValueDistribution is not defined when α is not a real number:

ExtremeValueDistribution is not defined when β is not a positive real number:

The substitution of invalid parameters into symbolic outputs gives results that are not meaningful:

Neat Examples  (1)

PDFs for different α values with CDF contours:

Wolfram Research (2007), ExtremeValueDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ExtremeValueDistribution.html (updated 2016).

Text

Wolfram Research (2007), ExtremeValueDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ExtremeValueDistribution.html (updated 2016).

CMS

Wolfram Language. 2007. "ExtremeValueDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ExtremeValueDistribution.html.

APA

Wolfram Language. (2007). ExtremeValueDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ExtremeValueDistribution.html

BibTeX

@misc{reference.wolfram_2024_extremevaluedistribution, author="Wolfram Research", title="{ExtremeValueDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ExtremeValueDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_extremevaluedistribution, organization={Wolfram Research}, title={ExtremeValueDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ExtremeValueDistribution.html}, note=[Accessed: 21-November-2024 ]}