ErlangDistribution[k,λ]
represents the Erlang distribution with shape parameter k and rate λ.


ErlangDistribution
ErlangDistribution[k,λ]
represents the Erlang distribution with shape parameter k and rate λ.
Details
- The probability density for value
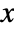 in an Erlang distribution is proportional to
in an Erlang distribution is proportional to 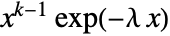 for
for 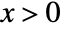 , and is zero for
, and is zero for 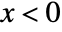 .
. - ErlangDistribution[k,λ] is equivalent to TransformedDistribution[x1+…+xk,…] with each xi from ExponentialDistribution[λ].
- ErlangDistribution allows k to be any positive integer and λ to be any positive real number.
- ErlangDistribution allows λ to be a quantity of any unit dimension, and k to be a dimensionless quantity. »
- ErlangDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- ErlangDistribution[k,λ] represents a continuous statistical distribution over the interval
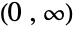 that is parametrized by two values k and λ. It is defined as the distribution of the sum
that is parametrized by two values k and λ. It is defined as the distribution of the sum  of k independent and identically distributed random variables
of k independent and identically distributed random variables  , each distributed as XiExponentialDistribution[λ]. Here, k is a positive integer and λ is a positive real-valued "service rate" that determines the overall height/steepness of the associated probability density function (PDF). The PDF of an Erlang distribution is continuous and may be either unimodal or monotonic decreasing, with a potential discontinuity approaching the lower boundary of its domain. In addition, the tails of the PDF are "fat", in the sense that the PDF decreases algebraically rather than decreasing exponentially for large values of
, each distributed as XiExponentialDistribution[λ]. Here, k is a positive integer and λ is a positive real-valued "service rate" that determines the overall height/steepness of the associated probability density function (PDF). The PDF of an Erlang distribution is continuous and may be either unimodal or monotonic decreasing, with a potential discontinuity approaching the lower boundary of its domain. In addition, the tails of the PDF are "fat", in the sense that the PDF decreases algebraically rather than decreasing exponentially for large values of 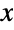 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.)
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) - The Erlang distribution was proposed by Danish mathematician and statistician Agner Krarup Erlang in the early 1900s as a tool to model phone call frequency. In the ensuing years, the Erlang distribution has become a regularly utilized tool in queueing theory, particularly for modeling a queue's conditional waiting time, given its current system state. For example, upon entering a queue that already has three people in it, the anticipated wait time
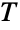 would satisfy TErlangDistribution[3,λ], where λ is the reciprocal of the mean service time per person.
would satisfy TErlangDistribution[3,λ], where λ is the reciprocal of the mean service time per person. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from an Erlang distribution. Distributed[x,ErlangDistribution[k,λ]], written more concisely as xErlangDistribution[k,λ], can be used to assert that a random variable x is distributed according to an Erlang distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[ErlangDistribution[k,λ],x] and CDF[ErlangDistribution[k,λ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with an Erlang distribution, EstimatedDistribution to estimate an Erlang parametric distribution from given data, and FindDistributionParameters to fit data to an Erlang distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Erlang distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Erlang distribution.
- TransformedDistribution can be used to represent a transformed Erlang distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain an Erlang distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Erlang distributions.
- The Erlang distribution is related to a number of other distributions, including the exponential distribution (through its definition). ErlangDistribution is also a special case of both GammaDistribution and PearsonDistribution, in the sense that the PDF of GammaDistribution[k, 1/λ] and PearsonDistribution[3, 1,(-k + 1)/λ, 0, 1/λ, 0] are both precisely the same as the PDF of ErlangDistribution[k,λ]. ErlangDistribution[k,λ] converges to NormalDistribution[k/λ,
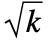 /λ] as k tends to Infinity, and ParetoDistribution can be obtained as a quotient of ExponentialDistribution and ErlangDistribution. Moreover, ErlangDistribution is related to a transformed ChiSquareDistribution, through which it inherits relationships with NormalDistribution, LogNormalDistribution, RayleighDistribution, WeibullDistribution, and MaxwellDistribution.
/λ] as k tends to Infinity, and ParetoDistribution can be obtained as a quotient of ExponentialDistribution and ErlangDistribution. Moreover, ErlangDistribution is related to a transformed ChiSquareDistribution, through which it inherits relationships with NormalDistribution, LogNormalDistribution, RayleighDistribution, WeibullDistribution, and MaxwellDistribution.
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from an Erlang distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness depends only on the parameter k:
As k grows, the distribution becomes more symmetric:
Kurtosis depends only on the parameter k:
As k grows, kurtosis nears the kurtosis of NormalDistribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (5)
Assume that the delay caused by a traffic signal is exponentially distributed with an average delay of 0.5 minutes. A driver has to drive a route that passes through seven unsynchronized traffic signals. Find the distribution for the delay passing all signals:
Hence the distribution for the sum of 7 independent exponential variables:
Find the probability that traffic signals cause a delay greater than 5 minutes:
Assume that the duration of telephone calls is exponentially distributed. The average length of a telephone call is 3.7 minutes. Find the probability that nine consecutive phone calls will be longer than 25 minutes:
Summing 9 independent phone call durations:
The probability that they last longer than 25 minutes:
Assume that the time delay in a logic element is exponentially distributed and that the average delay is ![]() seconds. The longest sequence of logic elements in a combinational logic network is six. Find the probability that delay through all six elements is longer than
seconds. The longest sequence of logic elements in a combinational logic network is six. Find the probability that delay through all six elements is longer than ![]() seconds:
seconds:
Summing 6 independent delay distributions:
The probability that the delay is longer than ![]() seconds:
seconds:
A device has 3 lifetime phases: A, B, and C. The time spent in each phase follows an exponential distribution with a mean time of 10 hours; after phase C, failure occurs. Find the distribution of the time to failure of this device:
Find the mean time to failure:
Find the probability that such a device would be operational for at least 40 hours:
Simulate time to failure for 30 independent devices:
A system starts with 10 devices; one is active and the remaining nine are on standby. The lifetime of each device has ExponentialDistribution with parameter ![]() . When a device fails, it is immediately replaced with another device if there is one still available. The lifetime of the system then follows the distribution:
. When a device fails, it is immediately replaced with another device if there is one still available. The lifetime of the system then follows the distribution:
Find the reliability of the system:
Find the average lifetime of this system:
Find the probability that the system will be operational for at least 5000 hours:
Properties & Relations (9)
Erlang distribution is closed under scaling by a positive factor:
Erlang distribution is closed under addition:
For ![]() identically distributed variables:
identically distributed variables:
ErlangDistribution[k,λ] converges to a normal distribution as k->∞:
Relationships to other distributions:
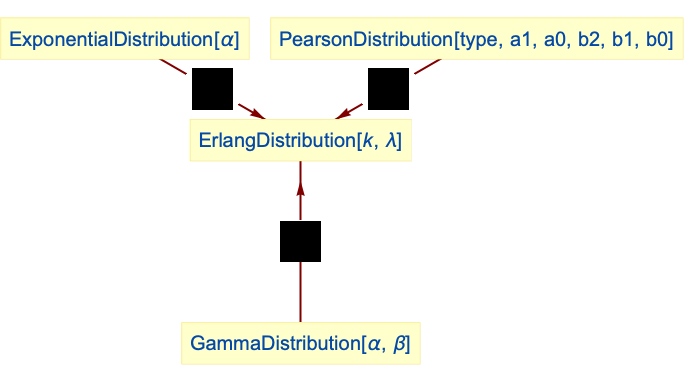
Sum of k variables with ExponentialDistribution is Erlang distributed:
Erlang distribution is a special case of type 3 PearsonDistribution:
Erlang distribution is a special case of GammaDistribution:
ParetoDistribution can be obtained as a quotient of ExponentialDistribution and ErlangDistribution:
ParetoDistribution can be obtained as a quotient of ErlangDistribution:
Text
Wolfram Research (2010), ErlangDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ErlangDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "ErlangDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ErlangDistribution.html.
APA
Wolfram Language. (2010). ErlangDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ErlangDistribution.html
BibTeX
@misc{reference.wolfram_2025_erlangdistribution, author="Wolfram Research", title="{ErlangDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ErlangDistribution.html}", note=[Accessed: 27-November-2025]}
BibLaTeX
@online{reference.wolfram_2025_erlangdistribution, organization={Wolfram Research}, title={ErlangDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ErlangDistribution.html}, note=[Accessed: 27-November-2025]}