GammaDistribution
GammaDistribution[α,β]
represents a gamma distribution with shape parameter α and scale parameter β.
GammaDistribution[α,β,γ,μ]
represents a generalized gamma distribution with shape parameters α and γ, scale parameter β, and location parameter μ.
Details
- The probability density for value
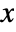 in a gamma distribution is proportional to
in a gamma distribution is proportional to 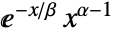 for
for 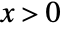 , and is zero for
, and is zero for 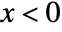 . »
. » - The probability density for value
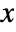 in a generalized gamma distribution is proportional to
in a generalized gamma distribution is proportional to 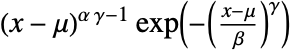 for
for 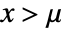 , and is zero elsewhere.
, and is zero elsewhere. - GammaDistribution allows α, β, and γ to be any positive real numbers and μ to be any real number.
- GammaDistribution allows β and μ to be any quantities of the same unit dimensions, and α, γ to be dimensionless quantities. »
- GammaDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- GammaDistribution[α,β,γ,μ] represents a continuous statistical distribution defined over the interval
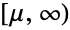 and parametrized by a real number μ (called a "location parameter"), two positive real numbers α and γ (called "shape parameters") and a positive real number β (called a "scale parameter"). The parameter μ determines the horizontal location of the probability density function (PDF) of the gamma distribution. The shape of the PDF is entirely dependent upon the combination of values taken by α, β, and γ and may be either unimodal or monotonically decreasing, with a potential singularity approaching the lower boundary of its domain. In addition, the tails of the PDF are "thin", in the sense that the PDF decreases exponentially for large values of
and parametrized by a real number μ (called a "location parameter"), two positive real numbers α and γ (called "shape parameters") and a positive real number β (called a "scale parameter"). The parameter μ determines the horizontal location of the probability density function (PDF) of the gamma distribution. The shape of the PDF is entirely dependent upon the combination of values taken by α, β, and γ and may be either unimodal or monotonically decreasing, with a potential singularity approaching the lower boundary of its domain. In addition, the tails of the PDF are "thin", in the sense that the PDF decreases exponentially for large values of 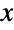 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The four-parameter version is sometimes referred to as the generalized gamma distribution, while the two-parameter form GammaDistribution[α,β] (which is equivalent to GammaDistribution[α,β,1,0]) is often referred to as "the" gamma distribution.
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The four-parameter version is sometimes referred to as the generalized gamma distribution, while the two-parameter form GammaDistribution[α,β] (which is equivalent to GammaDistribution[α,β,1,0]) is often referred to as "the" gamma distribution. - The (two-parameter) gamma distribution dates back to the 1830s work of Laplace, who obtained it as a posterior conjugate prior to distribution for the precision of normal variates, though the generalizations to three- and four-parameter forms can be traced back to Liouville's work on the Dirichlet integral formula. The name of the gamma distribution derives from the presence of the gamma function in its PDF. The gamma distribution is used to model a number of quantities across various fields. In statistics, the gamma distribution is the distribution associated with the sum of squares of independent unit normal variables and has been used to approximate the distribution of positive definite quadratic forms (i.e. those having the form
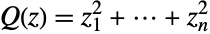 ) in multinormally distributed variables. The gamma distribution has also been used in many other fields, including meteorology, mathematical finance, statistical ecology, population dynamics, genomics, neuroscience, and actuarial science.
) in multinormally distributed variables. The gamma distribution has also been used in many other fields, including meteorology, mathematical finance, statistical ecology, population dynamics, genomics, neuroscience, and actuarial science. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a gamma distribution. Distributed[x,GammaDistribution[α,β,γ,μ]], written more concisely as xGammaDistribution[α,β,γ,μ], can be used to assert that a random variable x is distributed according to a gamma distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[GammaDistribution[α,β,γ,μ],x] and CDF[GammaDistribution[α,β,γ,μ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a gamma distribution, EstimatedDistribution to estimate a gamma parametric distribution from given data, and FindDistributionParameters to fit data to a gamma distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic gamma distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic gamma distribution.
- TransformedDistribution can be used to represent a transformed gamma distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a gamma distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving gamma distributions.
- The gamma distribution is related to several other distributions. As previously noted, GammaDistribution is firmly rooted in its relationship to NormalDistribution and MultinormalDistribution and is the conjugate prior (in Bayesian inference) to a handful of distributions, including PoissonDistribution, NormalDistribution, ExponentialDistribution, and GompertzMakehamDistribution. GammaDistribution generalizes ChiSquareDistribution (the PDF of GammaDistribution[ν/2,
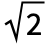 ,2,0] is the same as that of ChiSquareDistribution[ν]), ExponentialDistribution (the PDF of ExponentialDistribution[1/λ] is the same as that of GammaDistribution[1,λ]), and MaxwellDistribution (the PDF of MaxwellDistribution[σ] is precisely the same as GammaDistribution[3/2,
,2,0] is the same as that of ChiSquareDistribution[ν]), ExponentialDistribution (the PDF of ExponentialDistribution[1/λ] is the same as that of GammaDistribution[1,λ]), and MaxwellDistribution (the PDF of MaxwellDistribution[σ] is precisely the same as GammaDistribution[3/2,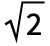 σ,2,0]). It can be transformed to obtain distributions such as InverseGammaDistribution, MoyalDistribution, and LogGammaDistribution. GammaDistribution is also related to PearsonDistribution, ErlangDistribution, BetaDistribution, ExpGammaDistribution, RayleighDistribution, ChiDistribution, WeibullDistribution, and StudentTDistribution.
σ,2,0]). It can be transformed to obtain distributions such as InverseGammaDistribution, MoyalDistribution, and LogGammaDistribution. GammaDistribution is also related to PearsonDistribution, ErlangDistribution, BetaDistribution, ExpGammaDistribution, RayleighDistribution, ChiDistribution, WeibullDistribution, and StudentTDistribution.
Examples
open allclose allBasic Examples (8)
Probability density function of a gamma distribution:
Cumulative distribution function of a gamma distribution:
Mean and variance of a gamma distribution:
Median of a gamma distribution:
Probability density function of a generalized gamma distribution:
Cumulative distribution function of a generalized gamma distribution:
Scope (12)
Generate a sample of pseudorandom numbers from a gamma distribution:
Compare its histogram to the PDF:
Generate a set of pseudorandom numbers that have generalized gamma distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness depends only on the shape parameters α and γ:
Skewness of gamma distribution:
In the limit, gamma distribution becomes symmetric:
Skewness of generalized gamma distribution:
Kurtosis depends only on the shape parameters α and γ:
Kurtosis of gamma distribution:
In the limit kurtosis nears the kurtosis of NormalDistribution:
Kurtosis of generalized gamma distribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Closed form for symbolic order:
Different moments of generalized gamma distribution:
Hazard function of a gamma distribution:
Hazard function of a generalized gamma distribution with ![]() :
:
Quantile function of a gamma distribution:
Quantile function of a generalized gamma distribution:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (6)
The lifetime of a device has gamma distribution. Find the reliability of the device:
The hazard function increasing in time for ![]() :
:
Find the reliability of two such devices in series:
Find the reliability of two such devices in parallel:
Compare the reliability of both systems for ![]() and
and ![]() :
:
A device has three lifetime stages: A, B, and C. The time spent in each phase follows an exponential distribution with a mean time of 10 hours; after phase C, a failure occurs. Find the distribution of the time to failure of this device:
Find the mean time to failure:
Find the probability that such a device would be operational for at least 40 hours:
Simulate time to failure for 30 independent devices:
In the morning rush hour, customers enter a coffee shop at a rate of 8 customers every 10 minutes. The time between customer arrivals follows an exponential distribution and the time between ![]() arrivals follows a GammaDistribution[k,1/λ] distribution. Find the probability of at least 40 customers arriving in 45 minutes:
arrivals follows a GammaDistribution[k,1/λ] distribution. Find the probability of at least 40 customers arriving in 45 minutes:
Find the average waiting time until the 40![]() customer arrives:
customer arrives:
Find the probability that the time until the 40![]() customer arrives is at least 1 hour:
customer arrives is at least 1 hour:
Simulate the waiting time until the 40![]() customer arrives during rush hour over 30 days:
customer arrives during rush hour over 30 days:
Mixtures of gamma distributions can be used to model multimodal data:
Histogram of waiting times for eruptions of the Old Faithful geyser exhibits two modes:
Fit a MixtureDistribution to the data:
Compare the histogram to the PDF of estimated distribution:
Find the probability that the waiting time is over 80 minutes:
Find most common waiting times:
Simulate waiting times for the next 60 eruptions:
LogNormalDistribution data can be modeled by a gamma distribution:
Compare the histogram to the PDF of estimated distribution:
Comparing log-likelihoods with estimation by lognormal distribution:
Stacy distribution is a special case of generalized GammaDistribution:
Properties & Relations (32)
Gamma distribution is closed under scaling by a positive factor:
Generalized gamma distribution is closed under translation and scaling by a positive factor:
Gamma distribution is closed under addition:
For ![]() identically distributed variables:
identically distributed variables:
GammaDistribution[α,β] converges to a normal distribution as α->∞:
Relationships to other distributions:
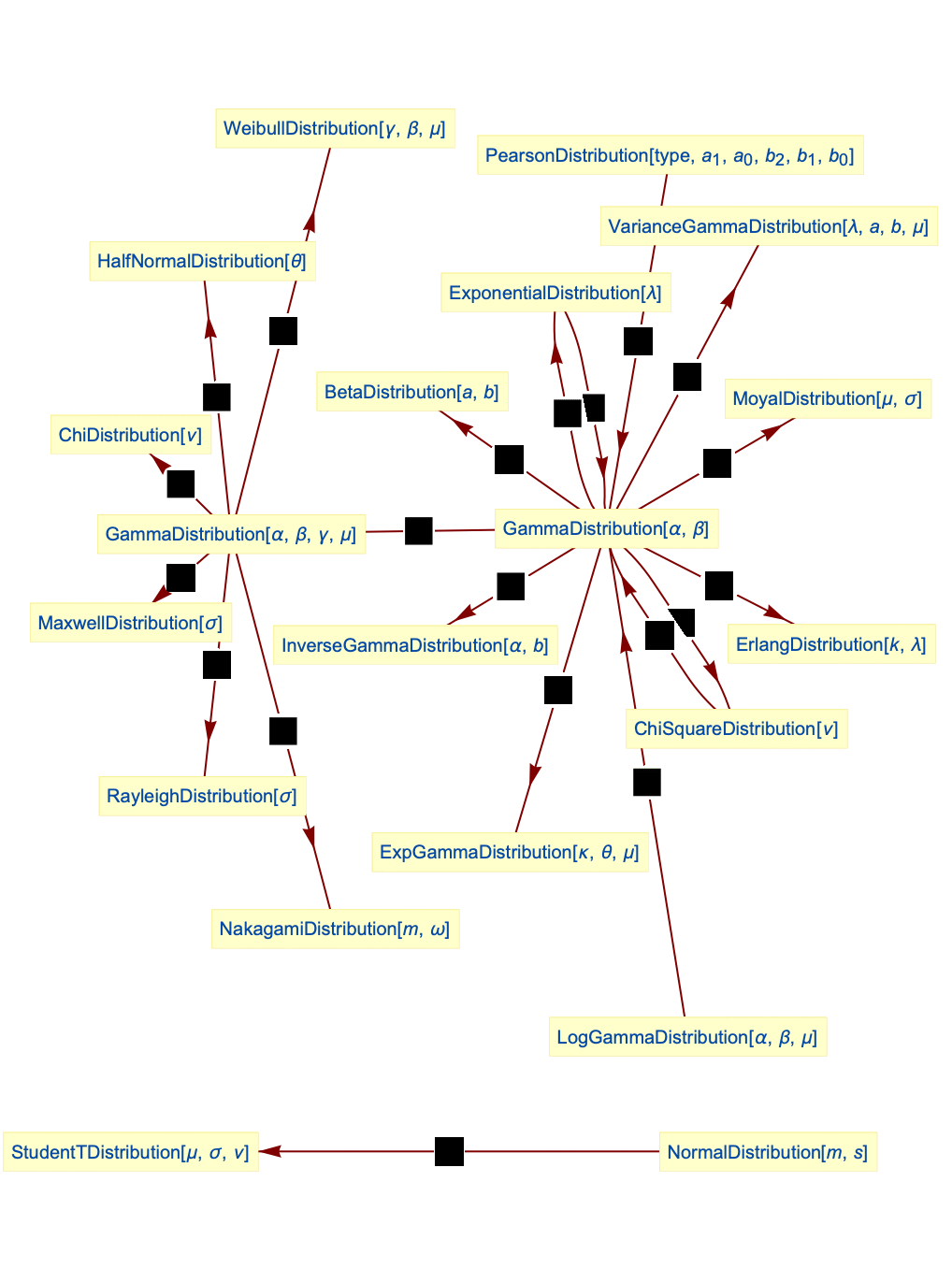
ChiSquareDistribution is a special case of gamma distribution:
Scaled ChiSquareDistribution follows gamma distribution:
ChiDistribution is a special case of GammaDistribution:
ExponentialDistribution is a special case of gamma distribution:
Sum of ![]() variates from ExponentialDistribution has gamma distribution:
variates from ExponentialDistribution has gamma distribution:
Gamma distribution and InverseGammaDistribution have an inverse relationship:
The generalized gamma distribution simplifies to a gamma distribution:
MaxwellDistribution is a special case of GammaDistribution:
MoyalDistribution is a transformation of a GammaDistribution:
RayleighDistribution is a special case of GammaDistribution:
NakagamiDistribution is a special case of GammaDistribution:
WeibullDistribution is a special case of generalized gamma distribution:
HalfNormalDistribution is a special case of generalized gamma distribution:
Generalized gamma distribution can be obtained as a transformation from gamma distribution:
ErlangDistribution is a special case of gamma distribution:
Gamma distribution is related to LogGammaDistribution:
GammaDistribution is related to ExpGammaDistribution:
BetaPrimeDistribution can be obtained as a quotient of generalized GammaDistribution:
ParetoDistribution can be obtained as a quotient of GammaDistribution:
GammaDistribution is a special case of type 3 PearsonDistribution:
BetaDistribution can be obtained as a transformation of two independent gamma variables:
KDistribution can be obtained from ExponentialDistribution and GammaDistribution:
Difference of gamma distributions follows VarianceGammaDistribution:
KDistribution can be represented as a parameter mixture of RayleighDistribution and GammaDistribution:
NegativeBinomialDistribution is a mixture of PoissonDistribution and GammaDistribution:
GeometricDistribution is a mixture of PoissonDistribution and GammaDistribution:
StudentTDistribution is a parameter mixture of a NormalDistribution with GammaDistribution:
ParetoDistribution can be obtained as a quotient of ExponentialDistribution and GammaDistribution:
Possible Issues (2)
GammaDistribution is not defined when either α or β is not a positive real number:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Text
Wolfram Research (2007), GammaDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/GammaDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "GammaDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/GammaDistribution.html.
APA
Wolfram Language. (2007). GammaDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GammaDistribution.html