BetaDistribution

BetaDistribution[α,β]

represents a continuous beta distribution with shape parameters α and β.

Details

The probability density for value 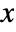in a beta distribution is proportional to 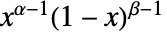for 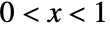, and is zero f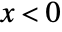or or . »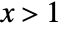
BetaDistribution allows α and β to be any positive real numbers.
BetaDistribution allows α and β to be dimensionless quantities. »
BetaDistribution can be used with such functions as Mean, CDF, and RandomVariate. »

Background & Context

BetaDistribution[α,β] represents a statistical distribution defined over the interval 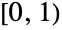and parametrized by two positive values α, β known as "shape parameters", which, roughly speaking, determine the "fatness" of the left and right tails in the probability density function (PDF). Depending on the values of α and β, the PDF of the beta distribution may be monotonic increasing, monotonic decreasing, or unimodal with potential singularities approaching the boundaries of its domain.
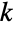
The beta distribution arises as a prior distribution for binomial proportions in Bayesian analysis. It is also commonly used to model random variables limited to a finite interval. For example, the distribution of the 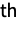smallest element in a continuous, independent, and uniformly distributed sample of size of 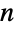can be computed using OrderDistribution[{UniformDistribution[],n},k] and is precisely equal to BetaDistribution[k,n-k+1]. In addition to its statistical significance, the beta distribution also plays a fundamental role in a number of scientific fields, including phenomena related to allele frequency distribution, soil property variability, geological mineral-to-rock ratios, and HIV transmission behavior.
RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a beta distribution. Distributed[x,BetaDistribution[α,β]], written more concisely as xBetaDistribution[α,β], can be used to assert that a random variable x is distributed according to a beta distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
The probability density and cumulative distribution functions may be given using PDF[BetaDistribution[α,β],x] and CDF[BetaDistribution[α,β],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
DistributionFitTest can be used to test if a given dataset is consistent with a beta distribution, EstimatedDistribution to estimate a beta parametric distribution from given data, and FindDistributionParameters to fit data to a beta distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic beta distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic beta distribution.
TransformedDistribution can be used to represent a transformed beta distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a beta distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving beta distributions.
The beta distribution is related to a number of other distributions. For example, BetaDistribution is the so-called "conjugate prior" for the parameters of a number of other distributions, including BernoulliDistribution, BinomialDistribution, NegativeBinomialDistribution, and GeometricDistribution. Moreover, BetaDistribution generalizes both UniformDistribution and PowerDistribution in the sense that (modulo inclusion of the endpoints and ), PDF[BetaDistribution[1,1],x] is equal to both PDF[UniformDistribution[],x] and PDF[PowerDistribution[1,1],x]. BetaDistribution can also be obtained as transformations of KumaraswamyDistribution and NoncentralBetaDistribution and is closely related to PERTDistribution, PearsonDistribution, ChiSquareDistribution, GammaDistribution, FRatioDistribution, and BetaPrimeDistribution.

Examples

open allclose all

Basic Examples (4)

Probability density function:

Cumulative distribution function:

Mean and variance:

Median:

Scope (8)

Generate a sample of pseudorandom numbers from a beta distribution:

Compare the histogram to the PDF:

Distribution parameters estimation:

Estimate the distribution parameters from sample data:

Compare a density histogram of the sample with the PDF of the estimated distribution:

Skewness varies with shape parameters:

When both parameters go to , the distribution becomes symmetric:

Kurtosis varies with shape parameters:

In the limit, the kurtosis becomes the same as for NormalDistribution:

Different moments with closed forms as functions of parameters:

Hazard function:

Quantile function:

Consistent use of Quantity in parameters expands them into their numeric values:

Find the mean:

Applications (3)

Cloud duration approximately follows a beta distribution with parameters 0.3 and 0.4 for a particular location. Find the probability that cloud duration will be longer than half a day:

Simulate the fraction of the day that is cloudy over a period of one month:

Find the average cloudiness duration for a day:

Find the probability of having exactly 20 days in a month with cloud duration less than 10%:

Find the probability of at least 20 days in a month with cloud duration less than 10%:

Beta distribution can be used to model the proportion of the stocks that increase in value on a given day. Fit beta distribution to the Dow Jones Industrial stocks data:

Find daily change:

Number of days for each financial entity:

Extract values from time series for each entity and normalize numeric quantities:

Check if each entity has the same length of data:

Calculate the daily ratio of companies with an increase in value:

Find fit, excluding days with no companies having an increase in value:

Compare the histogram of the data with the PDF of the estimated distribution:

Find the probability that at least 60% of Dow Jones Industrial stocks will increase in value:

Find the average percentage of Dow Jones Industrial stocks that will increase in value:

Simulate the percentage of Dow Jones Industrial stocks that will increase in value for 30 days:

Discrete-time Markov chain , where is the sequence of independent and identically distributed (iid) standard uniform random variables, and is the sequence of iid Bernoulli random variables with success probability of converges to stationary distribution BetaDistribution[p,1-p] for any initial condition such that :