DirichletDistribution
DirichletDistribution[{α1,…,αk+1}]
represents a Dirichlet distribution of dimension k with shape parameters αi.
Details
- DirichletDistribution is also known as multivariate beta distribution.
- The probability density for vector
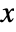 in a Dirichlet distribution is proportional to
in a Dirichlet distribution is proportional to 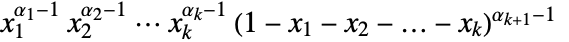 for
for 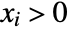 and
and  .
. - DirichletDistribution allows αi to be any positive real number.
- DirichletDistribution allows αi to be a dimensionless quantity.
- DirichletDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- DirichletDistribution[{α1,…,αk+1}] represents a continuous multivariate statistical distribution defined over k-tuples
 of positive real numbers whose sum is less than one and for which
of positive real numbers whose sum is less than one and for which 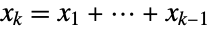 . The marginal distributions (MarginalDistribution) of DirichletDistribution[{α1,…,αk+1}] are all versions of BetaDistribution parametrized by various linear combinations of the components αi. As a result, the Dirichlet distribution is parametrized by a
. The marginal distributions (MarginalDistribution) of DirichletDistribution[{α1,…,αk+1}] are all versions of BetaDistribution parametrized by various linear combinations of the components αi. As a result, the Dirichlet distribution is parametrized by a 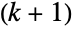 -tuple (α1,…,αk+1) whose components αi are all positive real numbers that together determine the overall shape of its probability density function (PDF). The Dirichlet distribution is sometimes referred to as the multivariate beta distribution.
-tuple (α1,…,αk+1) whose components αi are all positive real numbers that together determine the overall shape of its probability density function (PDF). The Dirichlet distribution is sometimes referred to as the multivariate beta distribution. - The PDF of a Dirichlet distribution has an absolute maximum at its mean, i.e. at the k-vector whose components are the one-variable means of its univariate marginal PDF. The tails of each of the associated marginal PDFs corresponding to a Dirichlet distribution are "fat," in the sense that the marginal PDF decreases algebraically for large values of
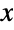 rather than decreasing exponentially. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of these distributions.)
rather than decreasing exponentially. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of these distributions.) - The Dirichlet distribution is named for German mathematician Johann Dirichlet. It has been used as a tool for modeling both real-world and theoretical phenomena since its formal introduction by Thomas Ferguson in the 1970s. The Dirichlet distribution is a finite version of the more general Dirichlet process, an infinite-dimensional stochastic process that, roughly speaking, assigns a probability distribution to each of a collection of probability distributions according to a specific algorithm. Similarly, the Dirichlet distribution often occurs as a prior distribution in Bayesian statistics, including as the conjugate prior for MultinomialDistribution. One interesting application of the Dirichlet distribution is in modeling randomness among accuracies of (fair) dice manufactured over time, noting that dice manufactured more recently tend to be "fairer" because of more precise manufacturing processes. The Dirichlet distribution has also been applied to data mining, machine learning, and computer vision. More recently, the Dirichlet distribution has been used to model the frequencies of words across collections of texts.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Dirichlet distribution. Distributed[{x1,…,xk},DirichletDistribution[{α1,…,αk+1}]], written more concisely as {x1,…,xk}DirichletDistribution[{α1,…,αk+1}], can be used to assert that a k-tuple (x1,…,xk) of random variables is distributed according to a Dirichlet distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[DirichletDistribution[{α1,…,αk+1}],{x1,…,xk}] and CDF[DirichletDistribution[{α1,…,αk+1}],{x1,…,xk}]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. Moreover, Covariance can be used to compute the covariance matrix corresponding to DirichletDistribution.
- DistributionFitTest can be used to test if a given dataset is consistent with a Dirichlet distribution, EstimatedDistribution to estimate a Dirichlet parametric distribution from given data, and FindDistributionParameters to fit data to a Dirichlet distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Dirichlet distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Dirichlet distribution.
- TransformedDistribution can be used to represent a transformed Dirichlet distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Dirichlet distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Dirichlet distributions.
- DirichletDistribution is closely related to a number of other distributions. As noted previously, DirichletDistribution has close ties with BetaDistribution, in the sense that each of its marginal distributions is a beta distribution. Moreover, any one-dimensional Dirichlet distribution is a beta distribution, in the sense that the PDF of DirichletDistribution[{α1,α2}] is precisely that of BetaDistribution[α1,α2]. DirichletDistribution is also related to GammaDistribution, in the sense that the random variable
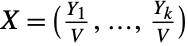 is distributed according to DirichletDistribution whenever
is distributed according to DirichletDistribution whenever 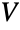 is the gamma-distributed random variable defined by the sum of k independently distributed gamma variates Y1,…,Yk. DirichletDistribution is the conjugate prior of MultinomialDistribution and is also related to BetaPrimeDistribution, CompoundPoissonDistribution, and MultinormalDistribution.
is the gamma-distributed random variable defined by the sum of k independently distributed gamma variates Y1,…,Yk. DirichletDistribution is the conjugate prior of MultinomialDistribution and is also related to BetaPrimeDistribution, CompoundPoissonDistribution, and MultinormalDistribution.
Examples
open allclose allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom vectors from a bivariate Dirichlet distribution:
Visualize the sample using a histogram:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Different mixed moments for a Dirichlet distribution:
Closed form for a symbolic order:
Univariate marginals of a Dirichlet distribution follow a BetaDistribution:
Multivariate marginals follow a DirichletDistribution:
Applications (5)
Show a distribution function and its histogram in the same plot:
Compare the PDF to its histogram version:
Compare the CDF to its histogram version:
Simulate points ![]() on the half-plane
on the half-plane ![]() with mean
with mean ![]() :
:
The point spread can be controlled by the third parameter:
Use Dirichlet distribution to define a multivariate Pólya distribution as a parameter mixture:
Find the probability over a Disk for a Dirichlet distribution:
Estimate confidence interval for maximum likelihood estimates of distribution parameters:
Apply fractional random weight bootstrap to estimate confidence interval, by repeating weighted estimation with weights sampled from a DirichletDistribution with unit parameters:
Generate a bootstrap sample of parameter estimates:
Visualize bootstrap estimates:
Fit BetaDistribution to the bootstrap parameters:
Properties & Relations (2)
Equal probability contours for a Dirichlet distribution:
One-dimensional Dirichlet distribution is a BetaDistribution:
Text
Wolfram Research (2010), DirichletDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/DirichletDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "DirichletDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/DirichletDistribution.html.
APA
Wolfram Language. (2010). DirichletDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DirichletDistribution.html