KumaraswamyDistribution
represents a Kumaraswamy distribution with shape parameters α and β.
Details
- The probability density for value
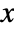 is proportional to
is proportional to 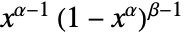 for
for 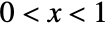 , and is zero elsewhere.
, and is zero elsewhere. - KumaraswamyDistribution allows α and β to be any positive real numbers.
- KumaraswamyDistribution allows α and β to be dimensionless quantities. »
- KumaraswamyDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- KumaraswamyDistribution[α,β] represents a statistical distribution supported on the interval
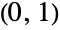 and parametrized by the positive real numbers α and β, known as "shape parameters", that determine the overall behavior of the probability density function (PDF). Depending on the values of α and β, the PDF of a Kumaraswamy distribution may have any of a number of shapes including unimodal with a single "peak" (i.e. a global maximum), monotone increasing, monotone decreasing, and "bathtub-shaped" (everywhere concave up with a global minimum) with potential singularities approaching the boundaries of its domain. The Kumaraswamy distribution is sometimes referred to as Kumaraswamy's double-bounded distribution and is sometimes considered "beta-like" because of the qualitative similarity of its PDF with that of the beta distribution (BetaDistribution).
and parametrized by the positive real numbers α and β, known as "shape parameters", that determine the overall behavior of the probability density function (PDF). Depending on the values of α and β, the PDF of a Kumaraswamy distribution may have any of a number of shapes including unimodal with a single "peak" (i.e. a global maximum), monotone increasing, monotone decreasing, and "bathtub-shaped" (everywhere concave up with a global minimum) with potential singularities approaching the boundaries of its domain. The Kumaraswamy distribution is sometimes referred to as Kumaraswamy's double-bounded distribution and is sometimes considered "beta-like" because of the qualitative similarity of its PDF with that of the beta distribution (BetaDistribution). - The Kumaraswamy distribution was developed by Indian hydrologist Poondi Kumaraswamy in a paper published in 1980 as a generalized distribution suitable for describing hydrological random variables not typically well-served by classical or empirical probability distributions. In particular, the Kumaraswamy distribution models random variates that are bounded on both sides and that may or may not have a mode existing between the two bounds. In addition to its theoretical importance, the Kumaraswamy distribution has wide applications throughout hydrology and other earth sciences and has been used to describe phenomena across various subfields of engineering including electrical, civil, mechanical, and financial engineering.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Kumaraswamy distribution. Distributed[x,KumaraswamyDistribution[α,β]], written more concisely as xKumaraswamyDistribution[α,β], can be used to assert that a random variable x is distributed according to a Kumaraswamy distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for Kumaraswamy distributions may be given using PDF[KumaraswamyDistribution[α,β],x] and CDF[KumaraswamyDistribution[α,β],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Kumaraswamy distribution, EstimatedDistribution to estimate a Kumaraswamy parametric distribution from given data, and FindDistributionParameters to fit data to a Kumaraswamy distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Kumaraswamy distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Kumaraswamy distribution.
- TransformedDistribution can be used to represent a transformed Kumaraswamy distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Kumaraswamy distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Kumaraswamy distributions.
- KumaraswamyDistribution is closely related to a number of other distributions. In addition to its qualitative relationship to BetaDistribution, KumaraswamyDistribution simplifies to BetaDistribution for certain values of its parameters (e.g. PDF[KumaraswamyDistribution[1,β],x] is the same as PDF[BetaDistribution[1,β],x], while PDF[KumaraswamyDistribution[α,1],x] is equal to PDF[BetaDistribution[α,1],x]). Similarly, KumaraswamyDistribution simplifies to PowerDistribution for certain parametrizations, while it can also be realized as a transformation (via TransformedDistribution) of BetaDistribution. KumaraswamyDistribution[1,1] is precisely UniformDistribution[{0,1}], and in general, KumaraswamyDistribution is related to ExponentialDistribution, PERTDistribution, PearsonDistribution, ChiSquareDistribution, GammaDistribution, FRatioDistribution, and BetaPrimeDistribution.
Examples
open allclose allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a Kumaraswamy distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Hazard function has a bathtub shape for ![]() :
:
Use dimensionless Quantity to define KumaraswamyDistribution:
Applications (1)
KumaraswamyDistribution can be used in hydrology; consider monthly water levels at Lake Mead:
According to the Arizona Game and Fish Department, the maximum lake level is 1229 feet:
Fit Kumaraswamy distribution to the relative water levels:
Compare the histogram of the data with the estimated distribution:
Find the probability that Lake Mead is below drought level (1125 feet):
Find the average water level in feet:
Simulate the water levels for the next three years (with respect to the drought level):
Properties & Relations (7)
Special transformations of KumaraswamyDistribution:
Relationships to other distributions:
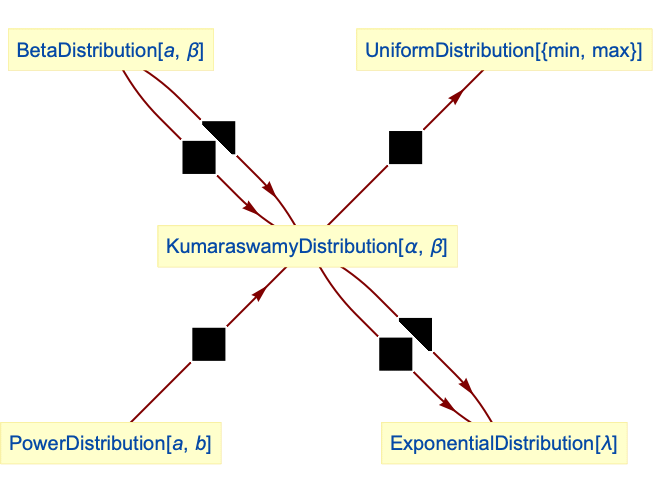
Kumaraswamy distribution is a transformation of a BetaDistribution:
Kumaraswamy distribution simplifies to a BetaDistribution:
Kumaraswamy distribution simplifies to a PowerDistribution:
UniformDistribution is a transformation of KumaraswamyDistribution:
ExponentialDistribution is a transformation of Kumaraswamy distribution:
Text
Wolfram Research (2010), KumaraswamyDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/KumaraswamyDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "KumaraswamyDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/KumaraswamyDistribution.html.
APA
Wolfram Language. (2010). KumaraswamyDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KumaraswamyDistribution.html