HistogramDistribution

HistogramDistribution[{x1,x2,…}]

represents the probability distribution corresponding to a histogram of the data values xi.

HistogramDistribution[{{x1,y1,…},{x2,y2,…},…}]

represents a multivariate histogram distribution based on data values {xi,yi,…}.

HistogramDistribution[…,bspec]

represents a histogram distribution with bins specified by bspec.

Details

  • HistogramDistribution returns a DataDistribution object that can be used like any other probability distribution.
  • The probability density function for HistogramDistribution for a value 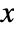is given by sum_(j=1)^m(c_j)/(n m_j) Boole[b_(j-1)<=x<b_j] where 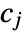is the number of data points in bin 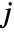, 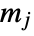is the width of bin 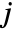, 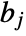are bin delimiters, and 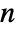is the total number of data points.
  • The 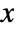width of each bin is computed according to the values xi, the 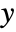width according to the yi, etc.
  • The following bin specifications bspec can be given:
  • nuse n bins
    {w}use bins of width w
    {min,max,w}use bins of width w from min to max
    {{b1,b2,…}}use bins [b1,b2),[b2,b3),…
    Automaticdetermine bin widths automatically
    "name"use a named binning method
    fwapply fw to get an explicit bin specification {b1,b2,…}
    {xspec,yspec,…}give different x, y, etc. specifications
  • Possible named binning methods include:
  • "FreedmanDiaconis"twice the interquartile range divided by the cube root of sample size
    "Knuth"balance likelihood and prior probability of a piecewise uniform model
    "Scott"asymptotically minimize the mean square error
    "Sturges"compute the number of bins based on the length of data
    "Wand"one-level recursive approximate Wand binning
  • The probability density for value 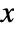in a histogram distribution is a piecewise constant function.
  • HistogramDistribution can be used with such functions as Mean, CDF, and RandomVariate.

Examples

open allclose all

Basic Examples  (2)

Create a histogram distribution of univariate data:

Use the resulting distribution to perform analysis, including visualizing distribution functions:

Compute moments and quantiles:

Create a histogram distribution of bivariate data:

Visualize the PDF and CDF:

Compute covariance and general moments:

Scope  (29)

Basic Uses  (5)

Create a distribution from a histogram of some data:

Compute probabilities from the distribution:

Create histogram distributions from quantity data:

Find select descriptive statistics:

Decrease the number of bins to decrease local sensitivity:

Increase the bin width to decrease local sensitivity:

Create distributions from histograms in higher dimensions:

Plot the univariate marginal PDFs:

Plot the bivariate marginal PDFs:

Distribution Properties  (10)

Estimate distribution functions:

Compute moments of the distribution:

Special moments:

General moments:

Quantile function:

Special quantile values:

Generate random numbers:

Compare with HistogramDistribution:

Compute probabilities and expectations:

Generating functions:

Estimate distribution functions for bivariate data:

Compute moments of a bivariate distribution:

Special moments:

General moments:

Generate random numbers:

Show the point distribution:

Having fewer bins yields a coarser approximation to the underlying distribution:

Generating functions:

Binning  (14)

Automatically compute the number of bins:

More data yields smaller bins:

Explicitly specify the number of bins to use:

Specify 5 and 50 bins, respectively:

Explicitly specify bin width:

Use bin widths 1. and 0.1:

Specify bin range and bin width:

Use bin widths of 1.5 and .15 respectively over fixed interval:

Provide explicit bin delimiters:

Use different automatic binning methods:

Delimit bins on integer boundaries using a binning function:

Automatically compute the number of bins for bivariate data:

More data yields smaller bins:

Explicitly specify the number of bins to use:

Explicitly specify bin width:

Specify bin range and bin width:

Explicitly give bin delimiters:

Use different automatic binning methods:

Use different bin specifications in each dimension:

Specify 3 bins in the row dimension and bin width 0.5 in the column dimension:

Applications  (6)

Compare an estimated density to a theoretical model:

Distribution of lengths of human chromosomes:

Compute the probability that the sequence length is greater than 15:

Compare the distributions of word length for some of the parts of speech:

The expected number of characters for a randomly chosen English noun:

Estimate the distribution of day-to-day point changes in the S&P 500 index:

Compute the probability of a 1% point change or more on a given day:

Determine the number of bins to use for bimodal data by Knuth's Bayesian method:

The optimal number of bins maximizes the log of the posterior density:

Density estimates using Knuth's method, Scott's rule, and the Freedman–Diaconis rule:

Knuth's method outperforms the other two in terms of LogLikelihood:

Construct a continuous version of the empirical cumulative distribution function:

Cumulative distribution function for HistogramDistribution is piecewise linear:

Compute Cramer–von Mises distance between the two distributions:

Properties & Relations  (10)

The PDF of HistogramDistribution is equivalent to a probability density Histogram:

The resulting density estimate integrates to unity:

The precision of the output matches the precision of the data:

The PDF is piecewise constant:

The CDF and SurvivalFunction are piecewise linear:

The HazardFunction is linear fractional:

HistogramDistribution is a MixtureDistribution of uniform distributions:

HistogramDistribution is a consistent estimator of the underlying distribution:

HistogramDistribution works with the values only when the input is a TimeSeries:

Compare to the histogram distribution of the values:

HistogramDistribution works with all the values together when the input is a TemporalData:

Compare to the histogram distribution calculated with the values from all the paths:

Possible Issues  (1)

It is possible to drop data from the estimation by specifying a binning range:

Specifying a width alone uses all the data:

Neat Examples  (1)

Random pop art with HistogramDistribution:

Wolfram Research (2010), HistogramDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/HistogramDistribution.html (updated 2016).

Text

Wolfram Research (2010), HistogramDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/HistogramDistribution.html (updated 2016).

CMS

Wolfram Language. 2010. "HistogramDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/HistogramDistribution.html.

APA

Wolfram Language. (2010). HistogramDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HistogramDistribution.html

BibTeX

@misc{reference.wolfram_2024_histogramdistribution, author="Wolfram Research", title="{HistogramDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/HistogramDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_histogramdistribution, organization={Wolfram Research}, title={HistogramDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/HistogramDistribution.html}, note=[Accessed: 21-November-2024 ]}