ConvolutionLayer

ConvolutionLayer[n,s]

represents a trainable convolutional net layer having n output channels and using kernels of size s to compute the convolution.

ConvolutionLayer[n,{s}]

represents a layer performing one-dimensional convolutions with kernels of size s.

ConvolutionLayer[n,{h,w}]

represents a layer performing two-dimensional convolutions with kernels of size h×w.

ConvolutionLayer[n,{h,w,d}]

represents a three-dimensional convolutions with kernels of size h×w×d.

ConvolutionLayer[n,kernel,opts]

includes options for padding and other parameters.

Details and Options

  • ConvolutionLayer[n,…] represents a layer that, applied to an input array with m input channels and one or more spatial dimensions, effectively performs n×m distinct convolutions across the spatial dimensions to produce an output array with n channels.
  • ConvolutionLayer[…][input] explicitly computes the output from applying the layer to input.
  • ConvolutionLayer[…][{input1,input2,…}] explicitly computes outputs for each of the inputi.
  • In ConvolutionLayer[n,s], the dimensionality of the convolution layer will be inferred when the layer is connected in a NetChain, NetGraph, etc.
  • The following optional parameters can be included:
  • "Biases"Automaticinitial vector of kernel biases
    "ChannelGroups" 1number of channel groups
    "Dilation" 1dilation factor
    "Dimensionality"Automaticnumber of spatial dimensions of the convolution
    Interleaving Falsethe position of the channel dimension
    LearningRateMultipliersAutomaticlearning rate multipliers for kernel weights and/or biases
    PaddingSize 0amount of zero padding to apply to the input
    "Stride" 1convolution step size to use
    "Weights"Automaticinitial array of kernel weights
  • The setting for PaddingSize can be of the following forms:
  • npad every dimension with n zeros on the beginning and end
    {n1,n2,…}pad the i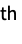^(th) dimension with n zeros on the beginning and end
    {{n1,m1},{n2,m2},…}pad the i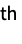^(th) dimension with ni zeros at the beginning and mi zeros at the end
    "Same"pad every dimension so that the output size is equal to the input size divided by the stride (rounded up)
  • The settings for "Dilation" and "Stride" can be of the following forms:
  • nuse the value n for all dimensions
    {…,ni,…}use the value ni for the i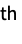^(th) dimension
  • By setting "ChannelGroups"g, the m input channels and n output channels are split into g groups of m/g and n/g channels, respectively, where m and n are required to be divisible by g. Separate convolutions are performed connecting the i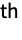^(th) group of input channels with the i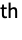^(th) group of output channels, and results are concatenated in the output. Each input/output group pair is connected by n/g×m/g convolutions, so setting "ChannelGroups"g effectively reduces the number of distinct convolutions from n×m to n×m/g.
  • The setting "Biases"None specifies that no biases should be used.
  • With the setting InterleavingFalse, the channel dimension is taken to be the first dimension of the input and output arrays.
  • With the setting InterleavingTrue, the channel dimension is taken to be the last dimension of the input and output arrays.
  • If weights and biases have been added, ConvolutionLayer[…][input] explicitly computes the output from applying the layer.
  • ConvolutionLayer[…][{input1,input2,…}] explicitly computes outputs for each of the inputi.
  • NetExtract can be used to extract weights and biases from a ConvolutionLayer object.
  • ConvolutionLayer is typically used inside NetChain, NetGraph, etc.
  • ConvolutionLayer exposes the following ports for use in NetGraph etc.:
  • "Input"an array of rank 2, 3 or 4
    "Output"an array of rank 2, 3 or 4
  • ConvolutionLayer can operate on arrays that contain "Varying" dimensions.
  • When it cannot be inferred from other layers in a larger net, the option "Input"{d1,…,dn} can be used to fix the input dimensions of ConvolutionLayer.
  • Given an input array of dimensions d1×…×di×…, the output array will be of dimensions 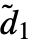×…××…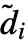, where the channel dimension 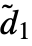=n and the sizes di are transformed according to 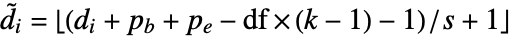, where 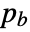/ 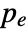are the padding sizes at the beginning/end of the axis, 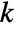is the kernel size, 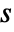is the stride size, and 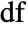is the dilation factor for each dimension.
  • Options[ConvolutionLayer] gives the list of default options to construct the layer. Options[ConvolutionLayer[…]] gives the list of default options to evaluate the layer on some data.
  • Information[ConvolutionLayer[…]] gives a report about the layer.
  • Information[ConvolutionLayer[…],prop] gives the value of the property prop of ConvolutionLayer[…]. Possible properties are the same as for NetGraph.

Examples

open allclose all

Basic Examples  (2)

Create a one-dimensional ConvolutionLayer with two output channels and a kernel size of 4:

Create an initialized one-dimensional ConvolutionLayer:

Apply the layer to an input matrix:

Scope  (11)

Ports  (3)

Create an initialized two-dimensional ConvolutionLayer:

Apply the layer to an input array:

The output is also a rank-3 array:

Create an initialized three-dimensional ConvolutionLayer with kernel size 2:

Apply the layer to an input array:

Create an initialized two-dimensional ConvolutionLayer that takes an RGB image and returns an RGB image:

Apply the layer to an image:

ConvolutionLayer automatically threads over batches of inputs:

Parameters  (7)

"Biases"  (3)

Create a two-dimensional ConvolutionLayer without biases:

Create a one-dimensional ConvolutionLayer with an identity kernel that applies a bias to the only channel:

Apply the layer to an input:

Create a two-dimensional ConvolutionLayer with an identity kernel that applies a bias to each channel:

Apply the layer to an image:

"Weights"  (4)

Create a one-dimensional ConvolutionLayer with a kernel that averages pairs from the input array:

Apply the layer to an input:

Create a two-dimensional ConvolutionLayer with three input channels and one output channel that applies a Gaussian blur:

Apply the layer to an image:

Create a two-dimensional ConvolutionLayer composed of per-channel Gaussian kernels. First create the kernels:

Visualize the kernels:

Initialize a net using the kernels:

Apply the layer to an image:

Create a two-dimensional ConvolutionLayer with a random kernel:

Apply the layer to an image:

Options  (12)

"ChannelGroups"  (2)

Create a two-dimensional ConvolutionLayer with three channel groups:

Using channel groups reduces the number of convolution weights by a factor equal to the group number. Check the dimensions of the weights:

Compare with the weight dimensions of an analogous layer with one channel group:

"Dilation"  (2)

A dilation factor of size n on a given dimension effectively applies the kernel to elements from the input arrays that are distance n apart.

Create a one-dimensional ConvolutionLayer with a dilation factor of 2:

Apply the layer to an input:

Create a random two-dimensional ConvolutionLayer with a dilation factor of 5:

Apply the dilated convolution layer to an image:

Interleaving  (1)

Create a ConvolutionLayer with InterleavingFalse and one input channel:

Create a ConvolutionLayer with InterleavingTrue and one input channel:

PaddingSize  (4)

Create a one-dimensional ConvolutionLayer that averages neighboring elements and pads with 4 zeros on each side:

Apply the layer to an input:

Create a random two-dimensional ConvolutionLayer that pads the first dimension with 10 zeros on each side and the second dimension with 25 zeros on each side:

Create a random two-dimensional ConvolutionLayer that pads the first dimension with 10 zeros at the beginning and 20 zeros at the end:

Use padding to make the output dimensions equivalent to the input dimensions:

This allows for deep networks to be defined with an arbitrary number of convolutions without the height and width of the input tending to 1.

"Stride"  (3)

A stride of size n on a given dimension effectively controls the step size with which the kernel is moved across the input array to produce the output array.

Create a one-dimensional ConvolutionLayer with a kernel that takes the average of neighboring pairs:

Apply the layer to an input:

Using a stride of 2 applies the kernel to non-overlapping pairs:

Using a stride of 4 applies the kernel to every other pair:

Create a random two-dimensional ConvolutionLayer with an asymmetric stride:

Apply the layer to an image:

Use a larger stride to reduce the dimension of the output:

A larger stride can also reduce computation time:

Properties & Relations  (2)

The following function computes the size of the non-channel dimensions, given the input size and parameters:

The output size of an input of size {256,252}, a kernel size of {2,3}, a stride of 2, a dilation factor of {3,4}, and a padding size of {1,2}:

ConvolutionLayer can be used to compute two-dimensional convolutions:

This is equivalent to ListConvolve after reversing the kernel:

Possible Issues  (3)

ConvolutionLayer cannot be initialized until all its input and output dimensions are known:

ConvolutionLayer cannot accept symbolic inputs:

The kernel size cannot be larger than the input dimensions:

Wolfram Research (2016), ConvolutionLayer, Wolfram Language function, https://reference.wolfram.com/language/ref/ConvolutionLayer.html (updated 2021).

Text

Wolfram Research (2016), ConvolutionLayer, Wolfram Language function, https://reference.wolfram.com/language/ref/ConvolutionLayer.html (updated 2021).

CMS

Wolfram Language. 2016. "ConvolutionLayer." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ConvolutionLayer.html.

APA

Wolfram Language. (2016). ConvolutionLayer. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConvolutionLayer.html

BibTeX

@misc{reference.wolfram_2024_convolutionlayer, author="Wolfram Research", title="{ConvolutionLayer}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/ConvolutionLayer.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_convolutionlayer, organization={Wolfram Research}, title={ConvolutionLayer}, year={2021}, url={https://reference.wolfram.com/language/ref/ConvolutionLayer.html}, note=[Accessed: 17-November-2024 ]}