Dendrogram
Dendrogram[{e1,e2,…}]
constructs a dendrogram from the hierarchical clustering of the elements e1, e2, ….
Dendrogram[{e1v1,e2v2,…}]
represents ei with vi in the constructed dendrogram.
Dendrogram[{e1,e2,…}{v1,v2,…}]
represents ei with vi in the constructed dendrogram.
Dendrogram[label1e1,label2e2,…]
represents ei using labels labeli in the constructed dendrogram.
Dendrogram[data,orientation]
constructs an oriented dendrogram according to orientation.
Dendrogram[tree]
constructs the dendrogram corresponding to weighted tree tree.
Details and Options


- The data elements ei can be numbers; numeric lists, matrices, or tensors; lists of Boolean elements; strings or images; geo positions or geographical entities; and colors, as well as combinations of these. If the ei are lists, matrices, or tensors, each must have the same dimensions.
- By default, Dendrogram is oriented from top to bottom. Possible orientations are: Top, Left, Right, and Bottom.
- Trees on which to compute Dendrogram can only be weighted on vertices.
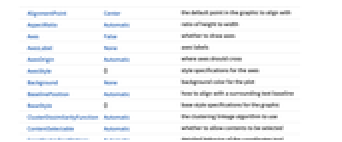
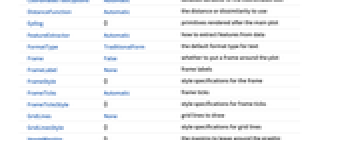
- Dendrogram has the same options as Graphics, with the following additions and changes: [List of all options]
-
ClusterDissimilarityFunction Automatic the clustering linkage algorithm to use DistanceFunction Automatic the distance or dissimilarity to use FeatureExtractor Automatic how to extract features from data - Dendrogram evaluated on a weighted tree only displays the graph as a dendrogram, therefore only the options of Graphics will change the final result.
- By default, Dendrogram will preprocess the data automatically unless either a DistanceFunction or a FeatureExtractor is specified.
- ClusterDissimilarityFunction defines the intercluster dissimilarity, given the dissimilarities between member elements.
- Possible settings for ClusterDissimilarityFunction include:
-
"Average" average intercluster dissimilarity "Centroid" distance from cluster centroids "Complete" largest intercluster dissimilarity "Median" distance from cluster medians "Single" smallest intercluster dissimilarity "Ward" Ward's minimum variance dissimilarity "WeightedAverage" weighted average intercluster dissimilarity a pure function - The function f defines a distance from any two clusters.
- The function f needs to be a real-valued function of the DistanceMatrix.
-
AlignmentPoint Center the default point in the graphic to align with AspectRatio Automatic ratio of height to width Axes False whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ClusterDissimilarityFunction Automatic the clustering linkage algorithm to use ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool DistanceFunction Automatic the distance or dissimilarity to use Epilog {} primitives rendered after the main plot FeatureExtractor Automatic how to extract features from data FormatType TraditionalForm the default format type for text Frame False whether to put a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelStyle {} style specifications for labels Method Automatic details of graphics methods to use PlotLabel None an overall label for the plot PlotRange All range of values to include PlotRangeClipping False whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RotateLabel True whether to rotate y labels on the frame Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks
List of all options

Examples
open allclose allBasic Examples (4)
Scope (7)
Obtain a dendrogram from a list of colors and display it to the left:
Compare the result with Dendrogram applied to the result of ClusteringTree:
Obtain a dendrogram from a heterogeneous dataset:
Compare it with the dendrogram of the colors:
Generate a sequence of random reals:
Obtain the dendrogram with the labeling given by the rounded reals:
Compute the dendrogram from an Association:
Compare it with the dendrogram of its Values:
Compare it with the dendrogram of its Keys:
Generate a dendrogram from a list of numbers:
Show the ![]() axis to compare distances between subclusters:
axis to compare distances between subclusters:
Generate a dendrogram from a list of vectors:
Display the result using vertical labeling:
Display the result using the ArrayPlot of the vectors as labeling:
Options (6)
AspectRatio (3)
By default, the ratio of the height to width for the plot is determined automatically:
Make the height the same as the width with AspectRatio1:
ClusterDissimilarityFunction (1)
DistanceFunction (1)
Generate a list of random vectors:
Obtain a dendrogram using the automatically chosen DistanceFunction and plot the ![]() axis:
axis:
Obtain a dendrogram using the EuclideanDistance and compare the values on the ![]() axis:
axis:
Obtain a dendrogram using a different DistanceFunction:
FeatureExtractor (1)
Obtain a dendrogram from a list of pictures:
Use a different FeatureExtractor to extract features:
Use the Identity FeatureExtractor to leave the data unchanged:
Applications (1)
Generate a list of random colors and compute its dendrogram with the distances on the y axis:
Compute the ClusteringTree for the same data by merging clusters that are closer than 0.65:
Compute the Dendrogram of the above graph:
Construct a Manipulate to visualize how clusters merge when the distance threshold increases:
Text
Wolfram Research (2016), Dendrogram, Wolfram Language function, https://reference.wolfram.com/language/ref/Dendrogram.html (updated 2017).
CMS
Wolfram Language. 2016. "Dendrogram." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/Dendrogram.html.
APA
Wolfram Language. (2016). Dendrogram. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Dendrogram.html