represents the dihedral group of order 2n.


DihedralGroup
represents the dihedral group of order 2n.
Details
- The degree n of DihedralGroup[n] must be a positive integer.
- DihedralGroup[1] is isomorphic to CyclicGroup[2] and represented by default as a permutation group on the points {1,2}.
- DihedralGroup[2] is isomorphic to AbelianGroup[{2,2}] and represented by default as a permutation group on the points {1,2,3,4}.
- For n≥3, DihedralGroup[n] is represented by default as a permutation group on the points {1,…,n}.
Background & Context
- DihedralGroup[n] represents the dihedral group
 of order
of order  (also denoted
(also denoted  or
or  ) for a given positive integer n. For
) for a given positive integer n. For  , the default representation of DihedralGroup[n] is as a permutation group on the symbols
, the default representation of DihedralGroup[n] is as a permutation group on the symbols  . The special cases DihedralGroup[1] and DihedralGroup[2] are isomorphic to CyclicGroup[2] and AbelianGroup[{2,2}], respectively, and are represented by default as a permutation group on the symbols
. The special cases DihedralGroup[1] and DihedralGroup[2] are isomorphic to CyclicGroup[2] and AbelianGroup[{2,2}], respectively, and are represented by default as a permutation group on the symbols  and
and  , respectively.
, respectively. - Mathematically, the dihedral group
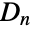 consists of the
consists of the 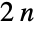 symmetries of a regular
symmetries of a regular 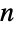 -gon, namely its
-gon, namely its  rotational symmetries and
rotational symmetries and  reflection symmetries. In particular,
reflection symmetries. In particular, 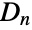 consists of elements
consists of elements  (rotations) and
(rotations) and 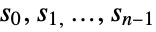 (reflections), which combine to transform under its group operation according to the identities
(reflections), which combine to transform under its group operation according to the identities  ,
,  ,
,  and
and  , where addition and subtraction are performed modulo
, where addition and subtraction are performed modulo 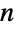 .
.  is a permutation group, but for
is a permutation group, but for  , the operations of reflection and rotation fail to commute in general, meaning
, the operations of reflection and rotation fail to commute in general, meaning  is nonabelian for
is nonabelian for  .
. - Dihedral groups are important in the analysis of regular structures, including in the determination of properties for symmetric chemical compounds and in crystallography.
- The usual group theoretic functions may be applied to DiherdalGroup[n], including GroupOrder, GroupGenerators, GroupElements and so on. A number of precomputed properties of the dihedral group
 are available via FiniteGroupData[{"DihedralGroup",n},"prop"].
are available via FiniteGroupData[{"DihedralGroup",n},"prop"]. - DihedralGroup is related to a number of other symbols. DihedralGroup[n] is isomorphic to the semidirect product of CyclicGroup[n] and CyclicGroup[2] (with the latter acting on the former by inversion), and for
 even, DihedralGroup[n] is isomorphic to the direct product of DihedralGroup[n/2] and CyclicGroup[2]. For
even, DihedralGroup[n] is isomorphic to the direct product of DihedralGroup[n/2] and CyclicGroup[2]. For  , the dihedral group
, the dihedral group  is a subgroup of the symmetric group
is a subgroup of the symmetric group  . Other infinite families of finite groups built into the Wolfram Language that are parametrized by integers include AbelianGroup, AlternatingGroup, CyclicGroup and SymmetricGroup.
. Other infinite families of finite groups built into the Wolfram Language that are parametrized by integers include AbelianGroup, AlternatingGroup, CyclicGroup and SymmetricGroup.
Examples
open all close allBasic Examples (3)
Scope (1)
DihedralGroup[n] for any positive integer n:
Properties & Relations (1)
DihedralGroup[1] and DihedralGroup[2] are the only dihedral commutative groups:
Possible Issues (1)
DihedralGroup[1] and DihedralGroup[2] are special as permutation groups because they are not subgroups of SymmetricGroup[1] and SymmetricGroup[2], respectively. Their permutation representations require larger supports:
Tech Notes
Related Guides
History
Text
Wolfram Research (2010), DihedralGroup, Wolfram Language function, https://reference.wolfram.com/language/ref/DihedralGroup.html.
CMS
Wolfram Language. 2010. "DihedralGroup." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DihedralGroup.html.
APA
Wolfram Language. (2010). DihedralGroup. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DihedralGroup.html
BibTeX
@misc{reference.wolfram_2025_dihedralgroup, author="Wolfram Research", title="{DihedralGroup}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/DihedralGroup.html}", note=[Accessed: 02-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_dihedralgroup, organization={Wolfram Research}, title={DihedralGroup}, year={2010}, url={https://reference.wolfram.com/language/ref/DihedralGroup.html}, note=[Accessed: 02-March-2026]}