SymmetricGroup

SymmetricGroup[n]

represents the symmetric group of degree n.

Details

  • The degree n of SymmetricGroup[n] must be a non-negative integer. Degrees 0 and 1 correspond to the trivial or identity group.
  • SymmetricGroup[n] is represented by default as a permutation group on the points {1,…,n}.

Background & Context

  • SymmetricGroup[n] represents the symmetric group 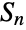(sometimes denoted 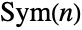) on n symbols for a given non-negative integer n. For 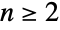, the default representation of SymmetricGroup[n] is as a permutation group on the symbols . The special cases SymmetricGroup[0] and SymmetricGroup[1] are equivalent to the trivial group with exactly one element.
  • Mathematically, the symmetric group 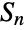(for 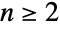) consists of the 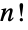permutations of the symbols together with the group operation of composition. Symmetric groups are therefore permutation groups of order 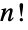with the elements of SymmetricGroup[n] coinciding with Permutations[Range[n]].
  • Symmetric groups are of fundamental importance in abstract algebra, geometric group theory, representation theory, combinatorics and mathematical physics. A number of important mathematical results hold for symmetric groups. For example, Cayley's theorem states that every abstract group is isomorphic to some subgroup of the symmetric group .
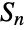  • The usual group theoretic functions may be applied to SymmetricGroup[n], including GroupOrder, GroupGenerators, GroupElements and so on. A number of precomputed properties of the symmetric group 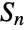are available via FiniteGroupData[{"SymmetricGroup",n},"prop"].
  • SymmetricGroup is related to a number of other symbols. Both alternating groups and dihedral groups are important subgroups of symmetric groups. Other infinite families of finite groups built into the Wolfram Language that are parametrized by integers include AbelianGroup, AlternatingGroup, CyclicGroup and DihedralGroup

Examples

open allclose all

Basic Examples  (3)

Number of elements of a symmetric group:

Permutation generators of a symmetric group:

Elements of a permutation representation of a symmetric group:

Scope  (1)

Symmetric groups of degree 0 or 1 are the trivial group, only containing the identity:

In all other cases, the symmetric group of degree n contains n! elements:

Applications  (1)

Test whether two random permutations generate the symmetric group of degree 100:

Properties & Relations  (1)

Permutations returns the permuted forms of an expression under the elements of a symmetric group:

Wolfram Research (2010), SymmetricGroup, Wolfram Language function, https://reference.wolfram.com/language/ref/SymmetricGroup.html.

Text

Wolfram Research (2010), SymmetricGroup, Wolfram Language function, https://reference.wolfram.com/language/ref/SymmetricGroup.html.

CMS

Wolfram Language. 2010. "SymmetricGroup." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SymmetricGroup.html.

APA

Wolfram Language. (2010). SymmetricGroup. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SymmetricGroup.html

BibTeX

@misc{reference.wolfram_2024_symmetricgroup, author="Wolfram Research", title="{SymmetricGroup}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/SymmetricGroup.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_symmetricgroup, organization={Wolfram Research}, title={SymmetricGroup}, year={2010}, url={https://reference.wolfram.com/language/ref/SymmetricGroup.html}, note=[Accessed: 30-December-2024 ]}