EccentricityCentrality
gives a list of eccentricity centralities for the vertices in the graph g.
EccentricityCentrality[{vw,…}]
uses rules vw to specify the graph g.
Details
- EccentricityCentrality will give high centralities to vertices that are at short maximum distances to every other reachable vertex.
- EccentricityCentrality for a graph g is given by
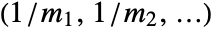 , where
, where 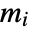 is the maximum distance from vertex
is the maximum distance from vertex 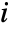 to all other vertices connected to
to all other vertices connected to 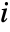 .
. - The eccentricity centrality for isolated vertices is taken to be zero.
- EccentricityCentrality works with undirected graphs, directed graphs, weighted graphs, multigraphs, and mixed graphs.
Background & Context
- EccentricityCentrality returns a list of non-negative machine numbers ("eccentricity centralities") that approximate particular centrality measures of the vertices of a graph. Eccentricity centrality is a measure of the centrality of a node in a network based on having a small maximum distance from a node
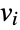 to every other reachable node (i.e. the graph eccentricities). This measure has found applications in social networks, transportation, biology, and the social sciences.
to every other reachable node (i.e. the graph eccentricities). This measure has found applications in social networks, transportation, biology, and the social sciences. - If
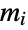 is the maximum distance from vertex
is the maximum distance from vertex 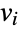 to all other vertices connected to
to all other vertices connected to 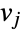 , then the eccentricity centralities are given by
, then the eccentricity centralities are given by 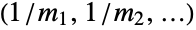 . The eccentricity centrality for isolated vertices is taken to be zero. Eccentricity centralities lie between 0 and 1 inclusive.
. The eccentricity centrality for isolated vertices is taken to be zero. Eccentricity centralities lie between 0 and 1 inclusive. - The eccentricity centrality of a vertex is the reciprocal of its VertexEccentricity. The full distance matrix of a graph can be computed using GraphDistanceMatrix.
Examples
open allclose allBasic Examples (2)
Scope (7)
EccentricityCentrality works with undirected graphs:
Use rules to specify the graph:
EccentricityCentrality works with large graphs:
Applications (5)
Rank vertices by their eccentricity:
Highlight the eccentricity centrality for CycleGraph:
Based on the infrastructure network of the Marshall Islands in eastern Micronesia, find a strategically located island:
It is different with the median of the graph:
A road network linking Chicago suburbs. Find the best location for hospitals and fire departments, to minimize the distance traveled by emergency vehicles:
For graphs with ![]() vertices, the largest sum in differences in eccentricity centrality between the most central vertex and all other vertices is the inverse of
vertices, the largest sum in differences in eccentricity centrality between the most central vertex and all other vertices is the inverse of ![]() :
:
Measure how central the most central vertex is with respect to other vertices:
Properties & Relations (6)
EccentricityCentrality is the inverse of maximum distances to other reachable vertices:
The inverse of maximum distances to other reachable vertices:
Eccentricity centrality of a vertex is the reciprocal of the VertexEccentricity:
Eccentricity centrality is between 0 and 1:
Eccentricity centralities for an undirected graph are equivalent to centralities for each component:
Computing the centralities for each component yields the same result:
Use GraphCenter to find vertices with the highest eccentricity centrality:
Use VertexIndex to obtain the centrality for a specific vertex:
Text
Wolfram Research (2012), EccentricityCentrality, Wolfram Language function, https://reference.wolfram.com/language/ref/EccentricityCentrality.html (updated 2015).
CMS
Wolfram Language. 2012. "EccentricityCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/EccentricityCentrality.html.
APA
Wolfram Language. (2012). EccentricityCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EccentricityCentrality.html