JacobiP
JacobiP[n,a,b,x]
gives the Jacobi polynomial ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- Explicit polynomials are given when possible.
![TemplateBox[{n, a, b, x}, JacobiP] TemplateBox[{n, a, b, x}, JacobiP]](Files/JacobiP.en/2.png) satisfies the differential equation
satisfies the differential equation 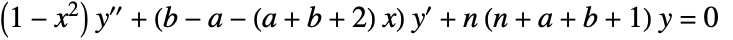 .
. - The Jacobi polynomials are orthogonal with weight function
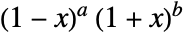 .
. - For certain special arguments, JacobiP automatically evaluates to exact values.
- JacobiP can be evaluated to arbitrary numerical precision.
- JacobiP automatically threads over lists.
- JacobiP[n,a,b,z] has a branch cut discontinuity in the complex z plane running from
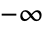 to
to 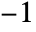 .
. - JacobiP can be used with Interval and CenteredInterval objects. »
Examples
open allclose allBasic Examples (7)
Compute the 2![]() Jacobi polynomial:
Jacobi polynomial:
Plot ![]() over a subset of the reals:
over a subset of the reals:
Plot over a subset of the complexes:
Series expansion at the origin:
Asymptotic expansion at Infinity:
Scope (39)
Numerical Evaluation (5)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
JacobiP can be used with Interval and CenteredInterval objects:
Specific Values (6)
Visualization (4)
Function Properties (11)
Domain of JacobiP of integer orders:
The range for JacobiP of integer orders:
The range for complex values is the whole plane:
JacobiP has the mirror property ![]() for integer
for integer ![]() ,
, ![]() and
and ![]() :
:
Jacobi polynomials are analytic functions:
However, ![]() is not an analytic function of
is not an analytic function of ![]() for noninteger
for noninteger ![]() ,
, ![]() and
and ![]() :
:
![]() is neither non-decreasing nor non-increasing:
is neither non-decreasing nor non-increasing:
![]() is increasing on its real domain:
is increasing on its real domain:
![]() is neither non-negative nor non-positive:
is neither non-negative nor non-positive:
![]() has no singularities or discontinuities for integer
has no singularities or discontinuities for integer ![]() ,
, ![]() and
and ![]() :
:
![]() is neither convex nor concave:
is neither convex nor concave:
![]() is concave on its real domain:
is concave on its real domain:
TraditionalForm formatting:
Differentiation (3)
Integration (3)
Compute the indefinite integral using Integrate:
Series Expansions (4)
Applications (4)
Expected value of the number of real eigenvalues of a complex matrix:
Solve a Jacobi differential equation:
Solution of the Schrödinger equation with a Pöschl–Teller potential:
Calculate the energy eigenvalue from the differential equation:
In an n-point Gauss–Radau quadrature rule, the value of one of the two extreme nodes is fixed, and the other n-1 nodes are computed from the roots of a certain Jacobi polynomial. Letting the leftmost node be the fixed node, compute the nodes and weights of an n-point Gauss–Radau quadrature rule:
Use the n-point Gauss–Radau quadrature rule to numerically evaluate an integral:
Compare the result of the Gauss–Radau quadrature with the result from NIntegrate:
Properties & Relations (2)
Text
Wolfram Research (1988), JacobiP, Wolfram Language function, https://reference.wolfram.com/language/ref/JacobiP.html (updated 2022).
CMS
Wolfram Language. 1988. "JacobiP." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/JacobiP.html.
APA
Wolfram Language. (1988). JacobiP. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JacobiP.html