MaxLimit

MaxLimit[f,xx*]

gives the max limit xx*f(x).

MaxLimit[f,{x1,…,xn}]

gives the nested max limit ⋯ f (x1,…,xn).

MaxLimit[f,{x1,…,xn}{,…,}]

gives the multivariate max limit f (x1,…,xn).

Details and Options

  • MaxLimit is also known as limit superior, supremum limit, limsup, upper limit and outer limit.
  • MaxLimit computes the smallest upper bound for the limit and is always defined for real-valued functions. It is often used to give conditions of convergence and other asymptotic properties where no actual limit is needed.
  • By using the character , entered as Mlim or \[MaxLimit], with underscripts or subscripts max limits can be entered as follows:
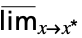  • fmax limit in the default direction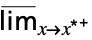
    fmax limit from above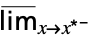
    fmax limit from below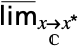
    fmax limit in the complex plane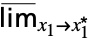
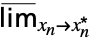    …fMaxLimit[f,{x1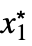,…,xn}]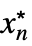
  • For a finite limit point x* and {,…,}:
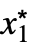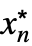  • MaxLimit[f,xx*]f* TemplateBox[{{max, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^*
    MaxLimit[f,{x1,…,xn}{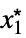,…,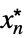}]f* TemplateBox[{{max, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^*
  • The definition uses the max envelope max[ϵ]==MaxValue[{f[x],0<TemplateBox[{{x, -, {x, ^, *}}}, Abs]<ϵ},x] for univariate f[x] and max[ϵ]==MaxValue[{f[x1,…,xn],0<TemplateBox[{{{, {{{x, _, {(, 1, )}}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]<ϵ},{x1,…,xn}] for multivariate f[x1,…,xn]. The function max[ϵ] is monotone decreasing as ϵ0, so it always has a limit, which may be ±∞.
  • The illustration shows max[TemplateBox[{{x, -, {x, ^, *}}}, Abs]] and max[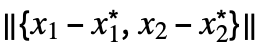] in blue.
  • For an infinite limit point x*∞, the max envelope max[ω]MaxValue[{f[x],x>ω},x] is used for univariate f and max[ω]MaxValue[{f[x1,…,xn],x1>ω∧⋯∧xn>ω},{x1,…,xn}] for multivariate f. The function max[ω] is monotone decreasing as ω∞, so it always has a limit.
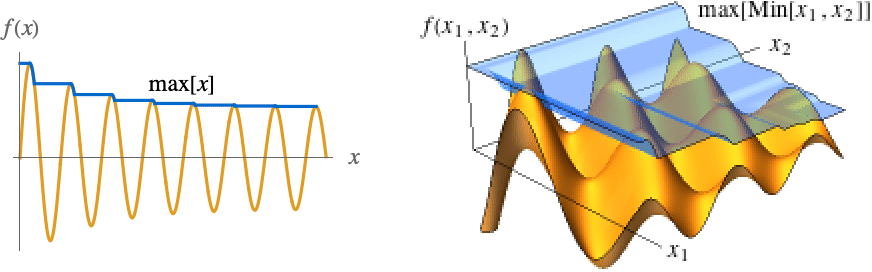
  • The illustration shows max[x] and max[Min[x1,x2]] in blue.
  • MaxLimit returns unevaluated when the max limit cannot be found.
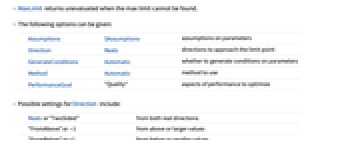
  • The following options can be given:
  • Assumptions$Assumptionsassumptions on parameters
    DirectionRealsdirections to approach the limit point
    GenerateConditionsAutomaticwhether to generate conditions on parameters
    MethodAutomaticmethod to use
    PerformanceGoal"Quality"aspects of performance to optimize
  • Possible settings for Direction include:
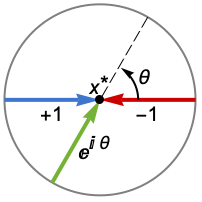
  • Reals or "TwoSided"from both real directions
    "FromAbove" or -1from above or larger values
    "FromBelow" or +1from below or smaller values
    Complexesfrom all complex directions
    Exp[ θ]in the direction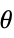
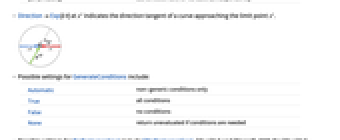
    {dir1,…,dirn}use direction diri for variable xi independently
  • DirectionExp[ θ] at x* indicates the direction tangent of a curve approaching the limit point x*.
  • Possible settings for GenerateConditions include:
  • Automaticnon-generic conditions only
    Trueall conditions
    Falseno conditions
    Nonereturn unevaluated if conditions are needed
  • Possible settings for PerformanceGoal include $PerformanceGoal, "Quality" and "Speed". With the "Quality" setting, MaxLimit typically solves more problems or produces simpler results, but it potentially uses more time and memory.

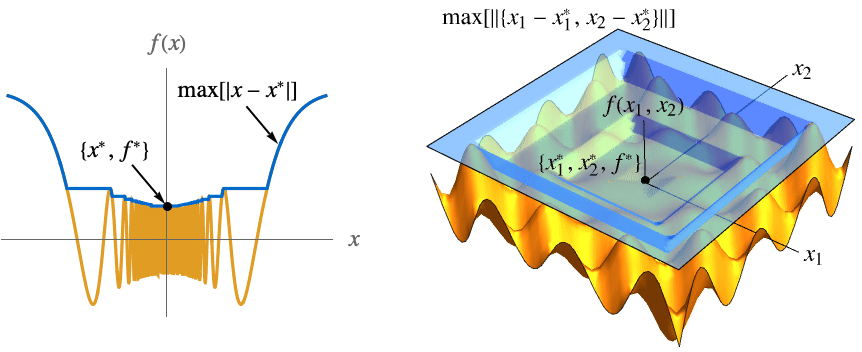
Examples

open allclose all

Basic Examples  (3)

A max limit at infinity:

The function gets closer and closer to 1 without ever touching it:

An infinite max limit:

Close to the discontinuity, there are arbitrarily large values:

Max limit from above:

Max limit from below:

The two-sided max limit is the larger of the two:

Scope  (35)

Basic Uses  (5)

Find the max limit at a point:

Find the max limit at a symbolic point:

Find the max limit at -Infinity:

The nested max limit as first and then :

The nested max limit as and then :

Compute the multivariate max limit as :

Typeset Limits  (4)

Use Mlim to enter the character, and to create an underscript:

Take a limit from above or below by using a superscript or on the limit point:

After typing zero, use to create a superscript:

To specify a direction of Reals or Complexes, enter the domain as an underscript on the character:

Enter the rule as ->, use to create an underscript, and type reals to enter :

TraditionalForm formatting:

Elementary Functions  (10)

Polynomials:

Rational functions at singular points:

Rational functions at ±Infinity:

Algebraic functions:

Trigonometric functions at singular points:

Trigonometric functions at ±Infinity:

Inverse trigonometric functions:

Exponential functions:

Logarithmic functions:

The function decays faster than any power of as :

Conversely, blows up faster than any power of :

Visualize representative functions:

Piecewise Functions  (5)

A discontinuous piecewise function:

A left-continuous piecewise function:

The two-sided max limit is the larger of the two:

UnitStep is effectively a right-continuous piecewise function:

RealSign is effectively a discontinuous piecewise function:

Note that TemplateBox[{0}, RealSign] is related to neither value:

Find the max limit of Floor as x approaches integer values:

Special Functions  (4)

Upper limits involving Gamma:

Upper limits involving Bessel-type functions:

Upper limits involving exponential integrals:

At every non-positive even integer, Gamma diverges to from one side:

Nested Max Limits  (3)

Compute the nested max limit as first and then :

The same result is obtained by computing two MaxLimit expressions:

Computing the max limit as first and then yields a different answer:

This is again equivalent to two nested max limits:

The nested max limit as first and then is :

The nested max limit as first and then is :

Consider the function for two variables at the origin:

The iterated max limit as and then is :

The iterated max limit as and then is :

The true bivariate max limit is , as points where almost cancels give arbitrarily large values:

For example, this value can be approached along the curve :

Visualize the function and the values along the two axes computed previously:

Multivariate Max Limits  (4)

Find the max limit of a multivariate function:

The two nested max limits give different answers:

Approaching the origin along the curve yields a third result:

The true two-dimensional max limit of the function is :

This is achieved along the curve :

Visualize the minimum and maximum values near the origin:

Find the max limit of a bivariate function:

The true two-dimensional max limit of the function is :

Note that neither iterated limit gives this result:

Indeed, along any rate the function is constant:

The maximum is approached along curves with close to , such as :

Visualize the function and the three max limits computed:

Find the max limit of a bivariate function at the origin:

The true two-dimensional max limit at the origin is :

Re-express the function in terms of polar coordinates:

The polar expression is bounded and disappears as , leaving the max limit of Sin:

Compute the max limit of a trivariate function:

The max limit at the origin is :

Note that the various iterated max limits are 0:

This is because the maximum is achieved along the line , :

The max limit can also be understood by transforming to spherical coordinates:

Visualize the function:

Options  (10)

Assumptions  (1)

Specify conditions on parameters using Assumptions:

Different assumptions can produce different results:

Direction  (5)

Max limit from below:

Equivalently:

Max limit from above:

Equivalently:

The default direction is Reals:

"TwoSided" is equivalent to Reals:

Max limit in the complex plane:

Compare with the limit over the reals:

Max limits at a branch cut:

Compute the bivariate max limit approach from different quadrants:

Approaching the origin from the first quadrant:

Equivalently:

Approaching the origin from the second quadrant:

Approaching the origin from the left half-plane:

Approaching the origin from the bottom half-plane:

Visualize the function:

GenerateConditions  (3)

Return a result without stating conditions:

This result is only valid if n>0:

Return unevaluated if the results depend on the value of parameters:

By default, conditions are generated that return a unique result:

By default, conditions are not generated if only special values invalidate the result:

With GenerateConditions->True, even these non-generic conditions are reported:

PerformanceGoal  (1)

Use PerformanceGoal to avoid potentially expensive computations:

The default setting uses all available techniques to try to produce a result:

Applications  (13)

Geometry of Max Limits  (3)

The function has a max limit of at :

This means there must be a sequence for which as ; for example, :

Numerically, and quite quickly:

Compute the two sequence limits exactly:

Note that this sequence limit exists even though itself does not have a limit as :

The function has the limit zero as approaches :

Thus, its max limit is zero:

In increasingly small regions around , gets increasingly flat and more of the graph is below :

The function does not have a limit as approaches :

However, its max limit is :

In increasingly small regions around , bounces wildly, but becomes a better and better ceiling for it:

Asymptotic Analysis  (3)

A function is said to be "big-o of " at , written , if _(x->_(TemplateBox[{}, Reals])a)TemplateBox[{{{(, {f, (, x, )}, )}, /, {(, {g, (, x, )}, )}}}, Abs]<infty:

For example, is :

But it is not :

The statement is always true:

If and , then :

It is possible for functions to share neither relationship:

Thus, is a reflexive partial order on functions:

if goes to zero at least as fast as :

From Taylor's theorem, if has continuous derivatives around , then :

This is the fifth-order Taylor polynomial at :

The definition of is _(x->_(TemplateBox[{}, Reals])a)TemplateBox[{{{(, {f, (, x, )}, )}, /, {(, {g, (, x, )}, )}}}, Abs]<infty:

Verify that :

Find the motion of a critically driven mass-spring system:

The motion is oscillatory but becomes arbitrarily large, indicating an instability:

Add overdamping the system:

The oscillatory motion is bounded and eventually restricted to +/-(TemplateBox[{alpha}, RealAbs])/betasqrt(k/m), indicating stability:

Continuity  (4)

A function is upper semicontinuous at if TemplateBox[{{f, (, x, )}, x, a}, MaxLimit2Arg]<=f(a). UnitStep is upper semicontinuous at the origin:

Visualize the function:

On the other hand, RealSign is not upper semicontinuous at the origin:

Visualize the function:

Consider the following function:

This function is upper semicontinuous at the origin:

This is despite f having neither a left nor a right limit at the origin:

Note that the MaxLimit of f does not depend on the value of f at zero, so any value greater than one would also make f upper semicontinuous:

Visualize f:

A function is lower semicontinuous at if TemplateBox[{{f, (, x, )}, x, a}, MinLimit2Arg]>=f(a). A real-valued function is continuous iff it is both upper and lower semicontinuous. SawtoothWave is lower semicontinuous at :

However, it is not upper semicontinuous, so it is discontinuous at the origin:

On the other hand, the following shows that TriangleWave is continuous at the origin:

Visualize the two functions:

Floor is discontinuous but upper semicontinuous at every integer:

On the other hand, Ceiling is neither continuous nor upper semicontinuous at the integers:

Both are continuous at noninteger values, but only Floor is upper semicontinuous on all of :

Differentiation  (3)

The left-upper Dini derivative is defined as:

The right-upper Dini derivative is defined similarly:

Ramp has finite upper Dini derivatives on the whole real line:

Note that these two derivatives are equal everywhere except the origin:

This is a reflection of the fact that Ramp is differentiable everywhere except the origin:

Consider the following function:

It is continuous at the origin:

But it has neither a left nor a right derivative:

It does, however, have finite Dini derivatives:

This indicates that the growth of the function around zero is bounded:

There are two right Dini derivatives. The first is the right-upper Dini derivative , defined as follows:

The right-lower Dini derivative is defined similarly using a min limit:

is right differentiable at if and only if the two are equal and finite, as in the case of Ramp at :

However, the function does not have a right derivative at the origin:

Properties & Relations  (13)

A real-valued function always has a (possibly infinite) max limit:

The corresponding limit does not exist:

Positive multiplicative constants can be moved outside a max limit:

If and have finite max limits as , then TemplateBox[{{(, {f, +, g}, )}, x, a}, MaxLimit2Arg]<=TemplateBox[{f, x, a}, MaxLimit2Arg]+TemplateBox[{g, x, a}, MaxLimit2Arg]:

In this case, there is strict inequality:

Assumptions apply to parameters in the max limit expression:

Direction places conditions on the limit variable:

When computing nested max limits, appropriate assumptions are generated on later limit variables:

Compare with the following:

For a real-valued function, if Limit exists, then MaxLimit has the same value:

If has a finite limit as , then TemplateBox[{{(, {f, +, g}, )}, x, a}, MaxLimit2Arg]=TemplateBox[{f, x, a}, MaxLimit2Arg]+TemplateBox[{g, x, a}, MaxLimit2Arg]:

MaxLimit is always greater than or equal to MinLimit:

If MaxLimit and MinLimit are equal, then the limit exists and equals their common value:

If the max limit is , then the min limit and thus the limit are also :

MaxLimit can be computed as -MinLimit[-f,…]:

If for , then TemplateBox[{{g, (, x, )}, x, a}, MaxLimit2Arg]<=TemplateBox[{{f, (, x, )}, x, a}, MinLimit2Arg]<=TemplateBox[{{f, , {(, x, )}}, x, a}, MaxLimit2Arg]:

If the two max limits are equal—as in this example—then has a limit as :

This is a generalization of the "squeezing" or "sandwich" theorem:

MaxLimit is always greater than or equal to DiscreteMaxLimit:

Possible Issues  (1)

MaxLimit is only defined for real-valued functions:

Neat Examples  (1)

Visualize a set of max limits:

Wolfram Research (2017), MaxLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/MaxLimit.html.

Text

Wolfram Research (2017), MaxLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/MaxLimit.html.

CMS

Wolfram Language. 2017. "MaxLimit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MaxLimit.html.

APA

Wolfram Language. (2017). MaxLimit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MaxLimit.html

BibTeX

@misc{reference.wolfram_2024_maxlimit, author="Wolfram Research", title="{MaxLimit}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/MaxLimit.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_maxlimit, organization={Wolfram Research}, title={MaxLimit}, year={2017}, url={https://reference.wolfram.com/language/ref/MaxLimit.html}, note=[Accessed: 21-December-2024 ]}