Search for all pages containing Median
- See Also
-
Related Guides
- Descriptive Statistics
- Survival Analysis
- Computation with Structured Datasets
- Probability & Statistics
- Time Series Processing
- Statistical Data Analysis
- Date & Time
- Math & Counting Operations on Lists
- Numerical Data
- Discrete & Integer Data
- Scientific Data Analysis
- Robust Descriptive Statistics
- Image Processing & Analysis
- Spatial Statistics
- Probability & Statistics with Quantities
- Tabular Transformation
- Tabular Modeling
- Audio Processing
- Tech Notes
-
- See Also
-
Related Guides
- Descriptive Statistics
- Survival Analysis
- Computation with Structured Datasets
- Probability & Statistics
- Time Series Processing
- Statistical Data Analysis
- Date & Time
- Math & Counting Operations on Lists
- Numerical Data
- Discrete & Integer Data
- Scientific Data Analysis
- Robust Descriptive Statistics
- Image Processing & Analysis
- Spatial Statistics
- Probability & Statistics with Quantities
- Tabular Transformation
- Tabular Modeling
- Audio Processing
- Tech Notes


Median
Details


- Median is a robust location estimator, which means it is not very sensitive to outliers.
- For VectorQ data
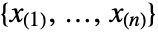 , the median can be thought of as the "middle value".
, the median can be thought of as the "middle value". - Formally, when data is sorted as
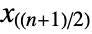 , the median is given by center element
, the median is given by center element 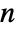 if
if 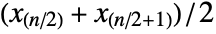 is odd and the mean of the two center elements
is odd and the mean of the two center elements 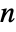 if
if  is even.
is even. - Median[data] is equivalent to Quantile[data,1/2,{{1/2,0},{0,1}}].
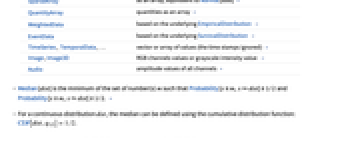
- For MatrixQ data, the median is computed for each column vector with Median[{{x1,y1,…},{x2,y2,…},…}] equivalent to {Median[{x1,x2,…}],Median[{y1,y2,…}],…}. »
- For ArrayQ data, median is equivalent to ArrayReduce[Median,data,1]. »
- The data can have the following additional forms and interpretations:
-
Association the values (the keys are ignored) » SparseArray as an array, equivalent to Normal[data] » QuantityArray quantities as an array » WeightedData based on the underlying EmpiricalDistribution » EventData based on the underlying SurvivalDistribution » TimeSeries, TemporalData, … vector or array of values (the time stamps ignored) » Image,Image3D RGB channels values or grayscale intensity value » Audio amplitude values of all channels » DateObject, TimeObject list of dates or list of times » - Median[dist] is the minimum of the set of number(s) m such that Probability[x≤m,xdist]≥1/2 and Probability[x≥m,xdist]≥1/2. »
- For a continuous distribution dist, the median can be defined using the cumulative distribution function:
![CDF[dist,q_(1/2)]=1/2 CDF[dist,q_(1/2)]=1/2](Files/Median.en/12.png) .
. - Median[dist] is equivalent to Quantile[dist,1/2].
- For a random process proc, the median function
 can be computed for slice distribution at time t, SliceDistribution[proc,t], as Median[SliceDistribution[proc,t]]. »
can be computed for slice distribution at time t, SliceDistribution[proc,t], as Median[SliceDistribution[proc,t]]. »



Examples
open all close allBasic Examples (4)
Scope (24)
Basic Uses (8)
Exact input yields exact output:
Approximate input yields approximate output:
Find the median of WeightedData:
Find the median of EventData:
Find the median of TemporalData:
Find the median of a TimeSeries:
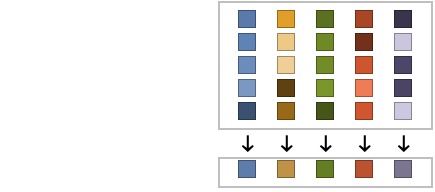
The median depends only on the values:
Array Data (5)
Median for a matrix gives columnwise medians:
Median for a tensor gives columnwise medians at the first level:
When the input is an Association, Median works on its values:
SparseArray data can be used just like dense arrays:
Find median of a QuantityArray:
Image and Audio Data (2)
Date and Time (5)
Applications (7)
The median represents the center of a distribution:
The median for a distribution without a single mode:
Find the median length, in miles, for 141 major rivers in North America:
Plot a Histogram for the data:
Probability that the length exceeds 90% of the median:
Smooth an irregularly spaced time series using a moving median:
Obtain a robust estimate of location when outliers are present:
Extreme values have a large influence on the Mean:
Compute medians for slices of a collection of paths of a random process:
Properties & Relations (7)
Median is equivalent to a parametrized Quantile:
For nearly symmetric samples, Median and Mean are nearly the same:
For univariate data, Median coincides with SpatialMedian:
The Median of absolute deviations from the Median is MedianDeviation:
MovingMedian is a sequence of medians:
For any distribution, there is InverseCDF[dist,1/2]=Median[dist]:
Similarly for InverseSurvivalFunction:
For a continuous distribution, there is CDF[dist,Median[dist]]=1/2:
Similarly for SurvivalFunction:
Possible Issues (2)
Neat Examples (1)
The distribution of Median estimates for 20, 100, and 300 samples:
Tech Notes
Related Guides
-
▪
- Descriptive Statistics ▪
- Survival Analysis ▪
- Computation with Structured Datasets ▪
- Probability & Statistics ▪
- Time Series Processing ▪
- Statistical Data Analysis ▪
- Date & Time ▪
- Math & Counting Operations on Lists ▪
- Numerical Data ▪
- Discrete & Integer Data ▪
- Scientific Data Analysis ▪
- Robust Descriptive Statistics ▪
- Image Processing & Analysis ▪
- Spatial Statistics ▪
- Probability & Statistics with Quantities ▪
- Tabular Transformation ▪
- Tabular Modeling ▪
- Audio Processing
History
Introduced in 2003 (5.0) | Updated in 2008 (7.0) ▪ 2016 (11.0) ▪ 2023 (13.3) ▪ 2024 (14.1)
Text
Wolfram Research (2003), Median, Wolfram Language function, https://reference.wolfram.com/language/ref/Median.html (updated 2024).
CMS
Wolfram Language. 2003. "Median." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Median.html.
APA
Wolfram Language. (2003). Median. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Median.html
BibTeX
@misc{reference.wolfram_2025_median, author="Wolfram Research", title="{Median}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Median.html}", note=[Accessed: 23-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_median, organization={Wolfram Research}, title={Median}, year={2024}, url={https://reference.wolfram.com/language/ref/Median.html}, note=[Accessed: 23-February-2026]}