MeyerWavelet
represents the Meyer wavelet of order 3.
MeyerWavelet[n]
represents the Meyer wavelet of order n evaluated on the equally spaced interval {-10,10}.
MeyerWavelet[n,lim]
represents the Meyer wavelet of order n evaluated on the equally spaced interval {-lim,lim}.
Details
- MeyerWavelet defines a family of orthonormal wavelets.
- MeyerWavelet[n] is equivalent to MeyerWavelet[n,8].
- MeyerWavelet[n,lim] is defined for any positive integer n and real limit lim.
- The scaling function (
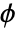) and wavelet function (
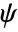) have infinite support. The functions are symmetric. - The scaling function (
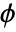) is given by its Fourier transform as ![1 TemplateBox[{omega}, Abs]<=(2 pi)/3; cos(1/2 pi nu((3 TemplateBox[{omega}, Abs])/(2 pi)-1)) (2 pi)/3<=TemplateBox[{omega}, Abs]<=(4 pi)/3](Files/MeyerWavelet.en/4.png "1 TemplateBox[{omega}, Abs]<=(2 pi)/3; cos(1/2 pi nu((3 TemplateBox[{omega}, Abs])/(2 pi)-1)) (2 pi)/3<=TemplateBox[{omega}, Abs]<=(4 pi)/3")
. » - The wavelet function (
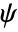) is given by its Fourier transform as ![exp((ⅈ omega)/2) sin(pi/2 nu((3 TemplateBox[{omega}, Abs])/(2 pi)-1)) (2 pi)/3<=TemplateBox[{omega}, Abs]<=(4 pi)/3; exp((ⅈ omega)/2) cos(pi/2 nu((3 TemplateBox[{omega}, Abs])/(4 pi)-1)) (4 pi)/3<=TemplateBox[{omega}, Abs]<=(8 pi)/3](Files/MeyerWavelet.en/6.png "exp((ⅈ omega)/2) sin(pi/2 nu((3 TemplateBox[{omega}, Abs])/(2 pi)-1)) (2 pi)/3<=TemplateBox[{omega}, Abs]<=(4 pi)/3; exp((ⅈ omega)/2) cos(pi/2 nu((3 TemplateBox[{omega}, Abs])/(4 pi)-1)) (4 pi)/3<=TemplateBox[{omega}, Abs]<=(8 pi)/3")
. - The polynomial
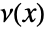is a polynomial of the form 
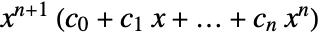, where 
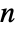is the order of the Meyer wavelet. - MeyerWavelet can be used with such functions as DiscreteWaveletTransform and WaveletPhi, etc.
Examples
open allclose allScope (9)
Basic Uses (4)
Wavelet Transforms (4)
Compute a DiscreteWaveletTransform:
View the tree of wavelet coefficients:
Get the dimensions of wavelet coefficients:
Plot the wavelet coefficients:
MeyerWavelet can be used to perform a DiscreteWaveletPacketTransform:
View the tree of wavelet coefficients:
Get the dimensions of wavelet coefficients:
Plot the wavelet coefficients:
MeyerWavelet can be used to perform a StationaryWaveletTransform:
View the tree of wavelet coefficients:
Get the dimensions of wavelet coefficients:
Plot the wavelet coefficients:
MeyerWavelet can be used to perform a StationaryWaveletPacketTransform:
View the tree of wavelet coefficients:
Properties & Relations (10)
Lowpass filter coefficients approximately sum to unity; 
:
Highpass filter coefficients approximately sum to zero; 
:
Scaling function integrates to unity; 
:
Wavelet function integrates to zero; 
:
satisfies the recursion equation 
:
Plot the components and the sum of the recursion:
satisfies the recursion equation 
:
Plot the components and the sum of the recursion:
Frequency response for 
is given by 
:
The filter is a lowpass filter:
Frequency response for 
is given by 
:
The filter is a highpass filter:
Fourier transform of 
is given by 
:
Compare the above result with the exact Fourier transform:
Text
Wolfram Research (2010), MeyerWavelet, Wolfram Language function, https://reference.wolfram.com/language/ref/MeyerWavelet.html.
CMS
Wolfram Language. 2010. "MeyerWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MeyerWavelet.html.
APA
Wolfram Language. (2010). MeyerWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeyerWavelet.html