SARMAProcess

SARMAProcess[{a1,…,ap},{b1,…,bq},{s,{α1,…,αm},{β1,…,βr}},v]

represents a weakly stationary seasonal autoregressive moving-average process with ARMA coefficients ai and bj, seasonal order s, seasonal ARMA coefficients αi and βj, and normal white noise with variance v.

SARMAProcess[{a1,…,ap},{b1,…,bq},{s,{α1,…,αm},{β1,…,βr}},Σ]

represents a weakly stationary vector SARMA process driven by normal white noise, with covariance matrix Σ.

SARMAProcess[{a1,…,ap},{b1,…,bq},{{s1,…},{α1,…,αm},{β1,…,βr}},Σ]

represents a weakly stationary vector SARMA process with multiple seasonal orders si.

SARMAProcess[{a1,…,ap},{b1,…,bq},{s,{α1,…,αm},{β1,…,βr}},v,init]

represents a SARMA process with initial data init.

SARMAProcess[c,…]

represents a SARMA process with a constant c.

Details

  • SARMAProcess is a discrete-time and continuous-state random process.
  • The SARMA process is described by the difference equation 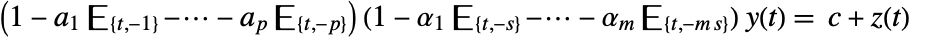, with 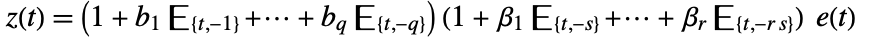, where is the state output, is white noise input, 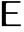is the shift operator, and the constant c is taken to be zero if not specified.
  • The initial data init can be given as a list {…,y[-2],y[-1]} or a single-path TemporalData object with time stamps understood as {…,-2,-1}.
  • A scalar SARMA process should have real coefficients ai, αi, bj, βj, and c, positive integer seasonality coefficients s, and a positive variance v.
  • An 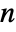-dimensional vector SARMA process should have real coefficient matrices ai, αi, bj, and βj of dimensions 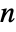×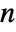, real vector c of length 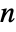, integer positive seasonality constants si or integer positive seasonality constant s, and the covariance matrix Σ should be symmetric positive definite of dimensions ×.
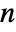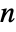  • The SARMA process with zero constant has transfer function 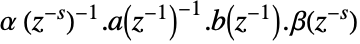, where 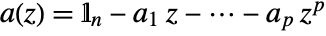, , 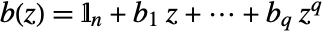, , 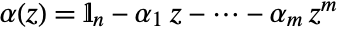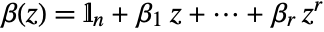and 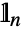is an n-dimensional unit.
  • SARMAProcess[p,q,{s,sp,sq}] represents a SARMA process with autoregressive and moving-average orders p and q, their seasonal counterparts sp and sq, and seasonality s for use in EstimatedProcess and related functions.
  • SARMAProcess can be used with such functions as CovarianceFunction, RandomFunction, and TimeSeriesForecast.

Examples

open allclose all

Basic Examples  (3)

Simulate a SARMA process:

Covariance function:

Correlation function:

Partial correlation function:

Scope  (33)

Basic Uses  (9)

Simulate an ensemble of paths:

Simulate with given precision:

Simulate a scalar process with different seasonalities:

Sample paths for positive and negative values of the parameter:

Simulate a weakly stationary process with given initial values:

For a process with a trend, initial values influence the behavior of the whole path:

Simulate a two-dimensional process:

Create a 2D sample path function from the data:

The color of the path is the function of time:

Create a 3D sample path function with time:

The color of the path is the function of time:

Simulate a three-dimensional process:

Create a sample path function from the data:

The color of the path is the function of time:

Estimate process parameters:

Compare the sample correlation functions with that of the estimated process:

Use TimeSeriesModel to automatically find orders:

Compare the sample covariance functions with the best time series model:

Forecast future values:

Find the forecast for the next 20 steps:

Show the path of the forecast:

Plot the data and the forecasted values:

Find a forecast for a vector-valued time series process:

Find the forecast for the next 15 steps:

Plot the data and the forecast for each component:

Covariance and Spectrum  (5)

Closed-form correlation function for low order:

Correlation matrix:

Covariance matrix:

Covariance function for a vector-valued process:

Power spectral density:

Vector SARMAProcess:

Stationarity and Invertibility  (4)

Check if a time series is weakly stationary:

For a vector process:

Find conditions for a process to be weakly stationary:

Stationarity conditions depend only on the autoregressive coefficients:

Check if a time series is invertible:

Find its invertible representation:

For a vector process:

Find invertibility conditions:

Estimation Methods  (5)

The available methods for estimating a SARMAProcess:

Method of moments admits the following solvers:

This method allows for fixed parameters:

Some relations between parameters are also permitted:

Maximum conditional likelihood method allows the following solvers:

This method allows for fixed parameters:

Some relations between parameters are also permitted:

Maximum likelihood method allows the following solvers:

This method allows for fixed parameters:

Some relations between parameters are also permitted:

Spectral estimator allows you to specify windows used for PowerSpectralDensity calculation:

Spectral estimator allows following solvers:

This method allows for fixed parameters:

Some relations between parameters are also permitted:

Process Slice Properties  (5)

Single time SliceDistribution:

Multiple time slice distributions:

Slice distribution of a vector-valued time series:

First-order stationary probability density function:

Stationary mean and variance:

Compare with the density function of a normal distribution:

Compute the expectation of an expression:

Calculate a probability:

Skewness and kurtosis:

Moment of order r:

Generating functions:

CentralMoment and its generating function:

FactorialMoment has no closed form for symbolic order:

Cumulant and its generating function:

Representations  (5)

Approximate with an ARProcess:

Compare the covariance function for the original and the approximate processes:

For a vector process:

Approximate with an MAProcess:

Compare sample paths:

For a vector process:

Represent as equivalent ARMAProcess:

Compare covariance functions:

TransferFunctionModel representation:

For a vector-valued process:

StateSpaceModel representation:

For a vector-valued process:

Applications  (3)

Use a SARMA process to model daily, monthly, and half-yearly autocorrelations:

The covariance function shows the serial correlations:

Daily mean temperature readings on the first of each month from the years 2000–2011 near your location:

Find process parameters:

The estimated time series process:

Forecast future values for the next three years:

Fit a SARMA model for the hourly measurements of temperature in August:

Find process parameters:

Check if the process is weakly stationary:

The SARMA model does capture the seasonal trend well:

Properties & Relations  (3)

SARMAProcess is a generalization of an ARMAProcess:

SARMAProcess is a generalization of an ARProcess:

SARMAProcess is a generalization of an MAProcess:

Possible Issues  (2)

Some properties are defined only for weakly stationary processes:

Use FindInstance to find a weakly stationary process:

ToInvertibleTimeSeries does not always exist:

There are zeros of TransferFunctionModel lying on the unit circle:

Neat Examples  (2)

Simulate a weakly stationary three-dimensional SARMAProcess:

Non-weakly stationary process, starting at the origin:

Simulate paths from a SARMA process:

Take a slice at 50 and visualize its distribution:

Plot paths and histogram distribution of the slice distribution at 50:

Wolfram Research (2012), SARMAProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/SARMAProcess.html (updated 2014).

Text

Wolfram Research (2012), SARMAProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/SARMAProcess.html (updated 2014).

CMS

Wolfram Language. 2012. "SARMAProcess." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/SARMAProcess.html.

APA

Wolfram Language. (2012). SARMAProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SARMAProcess.html

BibTeX

@misc{reference.wolfram_2024_sarmaprocess, author="Wolfram Research", title="{SARMAProcess}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/SARMAProcess.html}", note=[Accessed: 03-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_sarmaprocess, organization={Wolfram Research}, title={SARMAProcess}, year={2014}, url={https://reference.wolfram.com/language/ref/SARMAProcess.html}, note=[Accessed: 03-December-2024 ]}