The Internals of the Wolfram System
| Why You Do Not Usually Need to Know about Internals | The Software Engineering of the Wolfram System |
| Basic Internal Architecture | Testing and Verification |
| The Algorithms of the Wolfram Language |
Most of the documentation provided for the Wolfram System is concerned with explaining what the Wolfram System does, not how it does it. But the purpose of this is to say at least a little about how the Wolfram System does what it does. "Some Notes on Internal Implementation" gives more details.
You should realize at the outset that while knowing about the internals of the Wolfram System may be of intellectual interest, it is usually much less important in practice than you might at first suppose.
Indeed, one of the main points of the Wolfram System is that it provides an environment where you can perform mathematical and other operations without having to think in detail about how these operations are actually carried out inside your computer.
Thus, for example, if you want to factor the polynomial 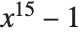 , you can do this just by giving Wolfram System the command Factor[x^15-1]; you do not have to know the fairly complicated details of how such a factorization is actually carried out by the internal code of the Wolfram System.
, you can do this just by giving Wolfram System the command Factor[x^15-1]; you do not have to know the fairly complicated details of how such a factorization is actually carried out by the internal code of the Wolfram System.
Indeed, in almost all practical uses of the Wolfram System, issues about how the Wolfram System works inside turn out to be largely irrelevant. For most purposes it suffices to view the Wolfram System simply as an abstract system which performs certain specified mathematical and other operations.
You might think that knowing how the Wolfram System works inside would be necessary in determining what answers it will give. But this is only very rarely the case. For the vast majority of the computations that the Wolfram System does are completely specified by the definitions of mathematical or other operations.
Thus, for example, 3^40 will always be 12157665459056928801, regardless of how the Wolfram System internally computes this result.
There are some situations, however, where several different answers are all equally consistent with the formal mathematical definitions. Thus, for example, in computing symbolic integrals, there are often several different expressions which all yield the same derivative. Which of these expressions is actually generated by Integrate can then depend on how Integrate works inside.
Here is the answer generated by Integrate:
This is an equivalent expression that might have been generated if Integrate worked differently inside:
In numerical computations, a similar phenomenon occurs. Thus, for example, FindRoot gives you a root of a function. But if there are several roots, which root is actually returned depends on the details of how FindRoot works inside.
With a different starting point, a different root is found. Which root is found with each starting point depends in detail on the internal algorithm used:
The dependence on the details of internal algorithms can be more significant if you push approximate numerical computations to the limits of their validity.
Thus, for example, if you give NIntegrate a pathological integrand, whether it yields a meaningful answer or not can depend on the details of the internal algorithm that it uses.
NIntegrate knows that this result is unreliable, and can depend on the details of the internal algorithm, so it prints warning messages:
Traditional numerical computation systems have tended to follow the idea that all computations should yield results that at least nominally have the same precision. A consequence of this idea is that it is not sufficient just to look at a result to know whether it is accurate; you typically also have to analyze the internal algorithm by which the result was found. This fact has tended to make people believe that it is always important to know internal algorithms for numerical computations.
But with the approach that the Wolfram System takes, this is rarely the case. For the Wolfram System can usually use its arbitrary‐precision numerical computation capabilities to give results where every digit that is generated follows the exact mathematical specification of the operation being performed.
Even though this is an approximate numerical computation, every digit is determined by the mathematical definition for 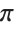 :
:
If you use machine‐precision numbers, the Wolfram System cannot give a reliable result, and the answer depends on the details of the internal algorithm used:
It is a general characteristic that whenever the results you get can be affected by the details of internal algorithms, you should not depend on these results. For if nothing else, different versions of the Wolfram System may exhibit differences in these results, either because the algorithms operate slightly differently on different computer systems, or because fundamentally different algorithms are used in versions released at different times.
Particularly in more advanced applications of the Wolfram System, it may sometimes seem worthwhile to try to analyze internal algorithms in order to predict which way of doing a given computation will be the most efficient. And there are indeed occasionally major improvements that you will be able to make in specific computations as a result of such analyses.
But most often the analyses will not be worthwhile. For the internals of the Wolfram System are quite complicated, and even given a basic description of the algorithm used for a particular purpose, it is usually extremely difficult to reach a reliable conclusion about how the detailed implementation of this algorithm will actually behave in particular circumstances.
A typical problem is that the Wolfram System has many internal optimizations, and the efficiency of a computation can be greatly affected by whether the details of the computation do or do not allow a given internal optimization to be used.
numbers | sequences of binary digits |
strings | sequences of character code bytes or byte pairs |
symbols | pointers to the central table of symbols |
general expressions | sequences of pointers to the head and elements |
When you type input into the Wolfram Language, a data structure is created in the memory of your computer to represent the expression you have entered.
In general, different pieces of your expression will be stored at different places in memory. Thus, for example, for a list such as {2,x,y+z} the "backbone" of the list will be stored at one place, while each of the actual elements will be stored at a different place.
The backbone of the list then consists just of three "pointers" that specify the addresses in computer memory at which the actual expressions that form the elements of the list are to be found. These expressions then in turn contain pointers to their subexpressions. The chain of pointers ends when one reaches an object, such as a number or a string, which is stored directly as a pattern of bits in computer memory.
Crucial to the operation of the Wolfram Language is the notion of symbols such as x. Whenever x appears in an expression, the Wolfram Language represents it by a pointer. But the pointer is always to the same place in computer memory—an entry in a central table of all symbols defined in your Wolfram Language session.
This table is a repository of all information about each symbol. It contains a pointer to a string giving the symbol's name, as well as pointers to expressions that give rules for evaluating the symbol.
Every piece of memory used by the Wolfram System maintains a count of how many pointers currently point to it. When this count drops to zero, the Wolfram System knows that the piece of memory is no longer being referenced, and immediately makes the piece of memory available for something new.
This strategy essentially ensures that no memory is ever wasted, and that any piece of memory that the Wolfram System uses is actually storing data that you need to access in your Wolfram System session.
■ Create an expression corresponding to the input you have given. |
■ Process the expression using all rules known for the objects in it. |
■ Generate output corresponding to the resulting expression. |
At the heart of the Wolfram Language is a conceptually simple procedure known as the evaluator, which takes every function that appears in an expression and evaluates that function.
When the function is one of the thousand or so that are built into the Wolfram Language, what the evaluator does is to execute directly internal code in the Wolfram Language. This code is set up to perform the operations corresponding to the function, and then to build a new expression representing the result.
A crucial feature of the built‐in functions in the Wolfram Language is that they support universal computation. What this means is that out of these functions you can construct programs that perform absolutely any kinds of operations that are possible for a computer.
As it turns out, small subsets of the Wolfram Language's built‐in functions would be quite sufficient to support universal computation. But having the whole collection of functions makes it in practice easier to construct the programs one needs.
The underlying point, however, is that because the Wolfram Language supports universal computation you never have to modify its built‐in functions: all you have to do to perform a particular task is to combine these functions in an appropriate way.
Universal computation is the basis for all standard computer languages. But many of these languages rely on the idea of compilation. If you use C or Fortran, for example, you first write your program, then you compile it to generate machine code that can actually be executed on your computer.
The Wolfram Language does not require you to go through the compilation step: once you have input an expression, the functions in the expression can immediately be executed.
Often the Wolfram Language will preprocess expressions that you enter, arranging things so that subsequent execution will be as efficient as possible. But such preprocessing never affects the results that are generated, and can rarely be seen explicitly.
The built‐in functions of the Wolfram Language implement a very large number of algorithms from computer science and mathematics. Some of these algorithms are fairly old, but the vast majority had to be created or at least modified specifically for the Wolfram Language. Most of the more mathematical algorithms in the Wolfram Language ultimately carry out operations which at least at some time in the past were performed by hand. In almost all cases, however, the algorithms use methods very different from those common in hand calculation.
Symbolic integration provides an example. In hand calculation, symbolic integration is typically done by a large number of tricks involving changes of variables and the like.
But in the Wolfram Language symbolic integration is performed by a fairly small number of very systematic procedures. For indefinite integration, the idea of these procedures is to find the most general form of the integral, then to differentiate this and try to match up undetermined coefficients.
Often this procedure produces at an intermediate stage immensely complicated algebraic expressions, and sometimes very sophisticated kinds of mathematical functions. But the great advantage of the procedure is that it is completely systematic, and its operation requires no special cleverness of the kind that only a human could be expected to provide.
In having the Wolfram Language do integrals, therefore, one can be confident that it will systematically get results, but one cannot expect that the way these results are derived will have much at all to do with the way they would be derived by hand.
The same is true with most of the mathematical algorithms in the Wolfram Language. One striking feature is that even for operations that are simple to describe, the systematic algorithms to perform these operations in the Wolfram Language involve fairly advanced mathematical or computational ideas.
Thus, for example, factoring a polynomial in 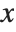 is first done modulo a prime such as 17 by finding the null space of a matrix obtained by reducing high powers of
is first done modulo a prime such as 17 by finding the null space of a matrix obtained by reducing high powers of 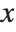 modulo the prime and the original polynomial. Then factorization over the integers is achieved by "lifting" modulo successive powers of the prime using a collection of intricate theorems in algebra and analysis.
modulo the prime and the original polynomial. Then factorization over the integers is achieved by "lifting" modulo successive powers of the prime using a collection of intricate theorems in algebra and analysis.
The use of powerful systematic algorithms is important in making the built‐in functions in the Wolfram Language able to handle difficult and general cases. But for easy cases that may be fairly common in practice it is often possible to use simpler and more efficient algorithms.
As a result, built‐in functions in the Wolfram Language often have large numbers of extra pieces that handle various kinds of special cases. These extra pieces can contribute greatly to the complexity of the internal code, often taking what would otherwise be a five‐page algorithm and making it hundreds of pages long.
Most of the algorithms in the Wolfram Language, including all their special cases, were explicitly constructed by hand. But some algorithms were instead effectively created automatically by computer.
Many of the algorithms used for machine‐precision numerical evaluation of mathematical functions are examples. The main parts of such algorithms are formulas which are as short as possible but which yield the best numerical approximations.
Most such formulas used in the Wolfram Language were actually derived by the Wolfram Language itself. Often many months of computation were required, but the result was a short formula that can be used to evaluate functions in an optimal way.
The Wolfram System is one of the more complex software systems ever constructed. It is built from several million lines of source code, written in C/C++, Java, and the Wolfram Language.
The C code in the Wolfram System is actually written in a custom extension of C which supports certain memory management and object‐oriented features. The Wolfram Language code is optimized using Share and DumpSave.
In the Wolfram Language kernel the breakdown of different parts of the code is roughly as follows: language and system: 30%; numerical computation: 20%; algebraic computation: 20%; graphics and kernel output: 30%.
Most of this code is fairly dense and algorithmic: those parts that are in effect simple procedures or tables use minimal code since they tend to be written at a higher level—often directly in the Wolfram System.
The source code for the kernel, save a fraction of a percent, is identical for all computer systems on which the Wolfram System runs.
For the front end, however, a significant amount of specialized code is needed to support each different type of user interface environment. The front end contains about 700,000 lines of system‐independent C++ source code, of which roughly 200,000 lines are concerned with expression formatting. Then there are between 50,000 and 100,000 lines of specific code customized for each user interface environment.
The Wolfram System uses a client‐server model of computing. The front end and kernel are connected via the Wolfram Symbolic Transfer Protocol (WSTP)—the same system as is used to communicate with other programs. WSTP supports multiple transport layers, including one based upon TCP/IP and one using shared memory.
The front end and kernel are connected via three independent WSTP connections. One is used for user-initiated evaluations. A second is used by the front end to resolve the values of Dynamic expressions. The third is used by the kernel to notify the front end of Dynamic objects which should be invalidated.
Within the C code portion of the Wolfram Language kernel, modularity and consistency are achieved by having different parts communicate primarily by exchanging complete Wolfram System expressions.
But it should be noted that even though different parts of the system are quite independent at the level of source code, they have many algorithmic interdependencies. Thus, for example, it is common for numerical functions to make extensive use of algebraic algorithms, or for graphics code to use fairly advanced mathematical algorithms embodied in quite different Wolfram System functions.
Since the beginning of its development in 1986, the effort spent directly on creating the source code for the Wolfram System is about a thousand developer‐years. In addition, a comparable or somewhat larger effort has been spent on testing and verification.
The source code of the Wolfram System has changed greatly since Version 1 was released. The total number of lines of code in the kernel grew from 150,000 in Version 1 to 350,000 in Version 2, 600,000 in Version 3, 800,000 in Version 4, 1.5 million in Version 5, and 2.5 million in Version 6. In addition, at every stage existing code has been revised—so that Version 6 has only a small percent of its code in common with Version 1.
Despite these changes in internal code, however, the user‐level design of the Wolfram System has remained compatible from Version 1 on. Much functionality has been added, but programs created for the Wolfram System Version 1 will almost always run absolutely unchanged under Version 6.
Every version of the Wolfram System is subjected to a large amount of testing before it is released. The vast majority of this testing is done by an automated system that is written in the Wolfram Language.
The automated system feeds millions of pieces of input to the Wolfram System, and checks that the output obtained from them is correct. Often there is some subtlety in doing such checking: one must account for different behavior of randomized algorithms and for such issues as differences in machine‐precision arithmetic on different computers.
- For every Wolfram Language function, inputs are devised that exercise both common and extreme cases.
- Inputs are devised to exercise each feature of the internal code.
- All the examples in the Wolfram Language's documentation system are used, as well as those from many books about the Wolfram System.
- Tests are constructed from mathematical benchmarks and test sets from numerous websites.
- Standard numerical tables are optically scanned for test inputs.
- Formulas from standard mathematical tables are entered.
- Exercises from textbooks are entered.
- For pairs of functions such as Integrate and D or Factor and Expand, random expressions are generated and tested.
When tests are run, the automated testing system checks not only the results, but also side effects such as messages, as well as memory usage and speed.
There is also a special instrumented version of the Wolfram System which is set up to perform internal consistency tests. This version of the Wolfram System runs at a small fraction of the speed of the real Wolfram System, but at every step it checks internal memory consistency, interruptibility, and so on.
The instrumented version of the Wolfram System also records which pieces of the Wolfram Language source code have been accessed, allowing one to confirm that all of the various internal functions in the Wolfram System have been exercised by the tests given.
All standard Wolfram System tests are routinely run on current versions of the Wolfram System, on each different computer system. Depending on the speed of the computer system, these tests take from a few hours to a few days of computer time.
Even with all this testing, however, it is inevitable in a system as complex as the Wolfram System that errors will remain.
The standards of correctness for the Wolfram System are certainly much higher than for typical mathematical proofs. But just as long proofs will inevitably contain errors that go undetected for many years, so also a complex software system such as the Wolfram System will contain errors that go undetected even after millions of people have used it.
Nevertheless, particularly after all the testing that has been done on it, the probability that you will actually discover an error in the Wolfram System in the course of your work is extremely low.
Doubtless there will be times when the Wolfram System does things you do not expect. But you should realize that the probabilities are such that it is vastly more likely that there is something wrong with your input to the Wolfram System or your understanding of what is happening than with the internal code of the Wolfram System itself.
If you do believe that you have found a genuine error in the Wolfram System, then you should contact Wolfram Research Technical Support, so that the error can be corrected in future versions.